در این قسمت از دوره رایگان آموزش متلب فنولوژی، در مورد انتگرال در متلب صحبت میکنیم. در قسمت قبلی مبحث حسابان و حد و مشتق در متلب را شروع کردیم. این قسمت نیز ادامهی قسمت قبل بوده و به بررسی انواع روشهای انتگرالگیری در متلب میپردازیم. با ما همراه باشید.
انواع انتگرال در متلب
در مبحث انتگرال گیری، به صورت عمده با دو نوع اساسی از انتگرالها سروکار داریم:
- انتگرال نامعین: در این نوع انتگرال، بازهی خاصی برای انتگرال گیری وجود ندارد و با داشتن مشتق یک تابع، به دنبال خود تابع یا تابع اولیه هستیم. به این عملیات که نوعی معکوس عملیات مشتق است، انتگرال نامعین میگویند و جواب نهایی یک تابع است.
- انتگرال معین: در انتگرال معین، یک بازهی مشخص داریم که روی آن بازه انتگرال یک تابع را حساب میکنیم و معمولا به یک جواب مشخص عددی میرسیم. از انتگرال معین در کاربردهای زیادی مانند یافتن محیط، مساحت، حجم، مرکز جرم و سایر کمیتهای اجسام استفاده میشود.
انتگرال نامعین در متلب
در انتگرال نامعین یک مقدار ثابت به تابع اولیه اضافه میشود و لذا انتگرال نامعین منحصر به فرد نیست. اگر تابع ۲x مشتق تابع اولیه باشد، برای یافتن انتگرال ۲x باید به دنبال تابعی باشیم که اگر از آن مشتق بگیریم به ۲x برسیم. این تابع میتواند x^2 باشد که با یک مقدار ثابت جمع میشود.
$ \int 2xdx = x^2 + c $
سینتکس انتگرال در متلب تابع int است. به مثال زیر توجه کنید:
|
1 2 |
syms x int(2*x) |
مشاهده نتیجه:
|
1 2 |
ans = x^2 |
مثال: در مثالهای زیر انواع رایج انتگرال در متلب را مشاهده میکنید. از تابع pretty برای تبدیل جواب به فرمت خواناتر استفاده شده است.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
syms x n a t int(x^n) f = sin(n*t) int(f) int(a*cos(pi*t)) int(a^x) int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)) |
با اجرای کد بالا نتایج زیر را مشاهده میکنید:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a) ans = sin(x) ans = exp(x) ans = x*(log(x) - 1) ans = log(x) ans = (24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5 2 4 24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x) ----------- + ------------- - -------------- + ------------ 3125 625 125 5 3 5 4 x sin(5 x) x sin(5 x) ------------- + ----------- 25 5 ans = -1/(4*x^4) ans = tan(x) 2 x (3 x - 5 x + 1) ans = - (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2 6 5 4 3 7 x 3 x 5 x x - ---- - ---- + ---- + -- 12 5 8 2 |
انتگرال معین در متلب
با تعریف ریاضی انتگرال، میدانیم که انتگرال معین در واقع حد یک مجموع است. با استفاده از انتگرال معین میتوان محیطی میان یک منحنی و محور xها را اندازه گیری کرد و یا محیط میان دو منحنی. به رابطهی زیر دقت کنید: (g تابع اولیه f و یا f مشتق g است)
$ \int_{a}^{b}f(x)dx=g(b)-g(a) $
برای انجام این انتگرال در متلب از سینتکس زیر استفاده میکنیم:
|
1 |
int(f(x), a, b) |
مثال ۱
انتگرال زیر را در نظر بگیرید. (با اجرای کد نتیجه ۶۵/۲ خواهد شد)
y=x در بازهی ۴ تا ۶
|
1 |
int(x, 4, 9) |
مثال ۲
در این مثال میخواهیم فضای بین محورxها و منحنی y = x3−۲x+5 را در بازهی x=1 تا x=2 حساب کنیم. یا به عبارتی هدف محاسبهی انتگرال زیر است:
$ \int_{1}^{2}(x^3-2x+5)dx $
فایل اسکریپت زیر را در متلب ایجاد کنید و اجرا کنید:
|
1 2 3 |
f = x^3 - 2*x +5; a = int(f, 1, 2) display('Area: '), disp(double(a)); |
با اجرای فایل بالا نتایج زیر را خواهید یافت:
|
1 2 3 4 |
a = 23/4 Area: 5.7500 |
مثال ۳
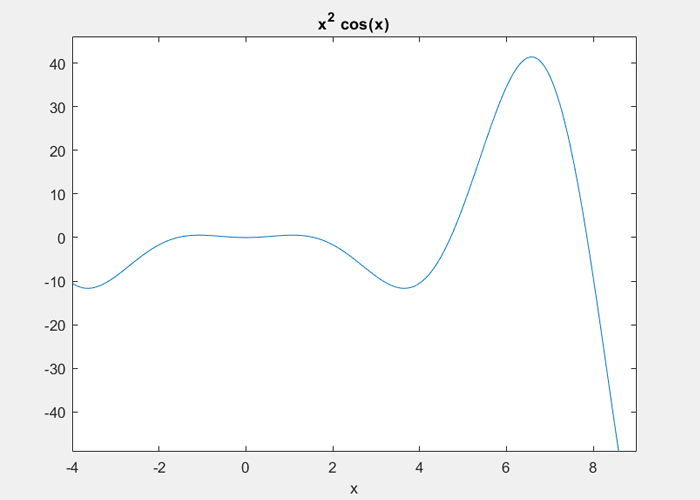
در این مثال میخواهیم مساحت زیر منحنی زیر را از -۴ تا ۹ حساب کنیم.
y=x^2cos(x)
|
1 2 3 4 |
f = x^2*cos(x); ezplot(f, [-4,9]) a = int(f, -4, 9) disp('Area: '), disp(double(a)); |
با اجرای کد تصویر زیر و خروجی را مشاهده میکنید:
|
1 2 3 4 5 |
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326 |
سینتکس انتگرال در octave
برای آشنایی با سینتکس انتگرال در octave مثال شماره ۲ را این بار به وسیلهی اکتاو حل میکنیم: (با دو روش)
روش اول:
|
1 2 3 4 5 6 7 8 9 10 |
pkg load symbolic symbols x = sym("x"); f = x^3 - 2*x +5; c = [1, 0, -2, 5]; integral = polyint(c); a = polyval(integral, 2) - polyval(integral, 1); display('Area: '), disp(double(a)); |
|
1 2 3 4 5 6 7 8 |
pkg load symbolic symbols x = sym("x"); f = inline("x^3 - 2*x +5"); [a, ierror, nfneval] = quad(f, 1, 2); display('Area: '), disp(double(a)); |
|
1 2 3 |
Area: 5.7500 |







