مشتق در متلب |‌ MATLAB calculus10 دقیقه مطالعه

هدیه فنولوژی به شما!

در این قسمت از دوره رایگان آموزش متلب فنولوژی،‌ در مورد حسابان و حد و مشتق در متلب صحبت می‌کنیم. همچنین در ادامه به حل برخی معادلات دیفرانسیل در متلب نیز می‌پردازیم. با ما همراه باشید.

محتوا پنهان‌سازی

1. حسابان در متلب

2. محاسبه مشتق در متلب

3. محاسبه حد در متلب

4. حد چپ و راست در متلب

5. بررسی قوانین مشتق در متلب

6. مشتقات توابع نمایی، لگاریتمی و مثلثاتی

7. محاسبه مشتقات مرتبه بالاتر

8. یافتن ماکسیمم و مینیمم‌های یک منحنی

9. حل معادلات دیفرانسیل در متلب

9.1. مثال معادله مرتبه اول و مرتبه دوم

10. سینتکس مشتق و حد در octave

حسابان در متلب

متلب یکی از بهترین ابزارهای حل معادلات دیفرانسیل و بررسی مسائل حساب، دیفرانسیل و انتگرال است. با داشتن یک تابع، شما می‌توانید به سادگی و زیبایی آن را در متلب رسم کنید،‌ و با داشتن نمودار اقدام به محاسبه‌ی مینیمم، ماکسیمم، و سایر نقاط مهم در نمودار کنید و همچنین با داشتن خواص مشتق و حد نمودار در نقاط مختلف آن را تحلیل کنید. در این قسمت در مورد محاسبه‌ی حد و مشتق در متلب صحبت می‌کنیم و در قسمت بعدی به محاسبه‌ی انتگرال در متلب می‌پردازیم.

محاسبه مشتق در متلب

متلب دستور diff را برای محاسبه مشتقات نمادین ارائه می‌دهد. در ساده‌ترین شکل، تابعی را که می‌خواهید مشتق بگیرید، به دستور diff واگذار می‌کنید.

برای مثال، اجازه دهید مشتق تابع f (t) = 3t^2 + 2t^-2 را محاسبه کنیم. یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ کنید:

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

syms t

f = 3*t^2 + 2*t^(-2);

diff(f)

مشاهده نتیجه:

ans =
6*t - 4/t^3

1 2	ans = 6*t - 4/t^3

تمرین برنامه نویسی

محاسبه حد در متلب

متلب برای محاسبه‌ی حد،‌ از تابع limit استفاده می‌کند. در ساده‌ترین حالت، این تابع متغیر x را در نقطه‌ی صفر بررسی می‌کند و حد آن‌ را نمایش می‌دهد. به مثال زیر توجه کنید:

syms x
limit((x^3 + 5)/(x^4 + 7))

1 2	syms x limit((x^3 + 5)/(x^4 + 7))

متلب حد تابع $f(x) = \frac{(x^3 + 5)}{(x^4 + 7)}$ را در نقطه‌ی صفر محاسبه می‌کند که جواب به صورت ans = 5/7 خواهد بود.

در سینتکس بالا با دستور syms به متلب می‌فهمانیم که x از نظر ما یک متغیر ریاضی است. اگر بخواهید حد تابع را در نقطه‌ای به جز صفر حساب کنید،‌ کافیست عددی که می‌خواهید حد را در آن نقطه محاسبه کنید به عنوان دومین آرگومان بیاورید. به مثال زیر توجه کنید:

syms x
limit((x - 3)/(x-1),1)

1 2	syms x limit((x - 3)/(x-1),1)

دستور بالا حد تابع $ f(x) = \frac{x-3}{x-1} $ را در نقطه‌ی یک محاسبه می‌کند که وجود ندارد (بی‌نهایت می‌شود) و متلب نتیجه‌ی ans = NaN را برمی‌گرداند.

حد چپ و راست در متلب

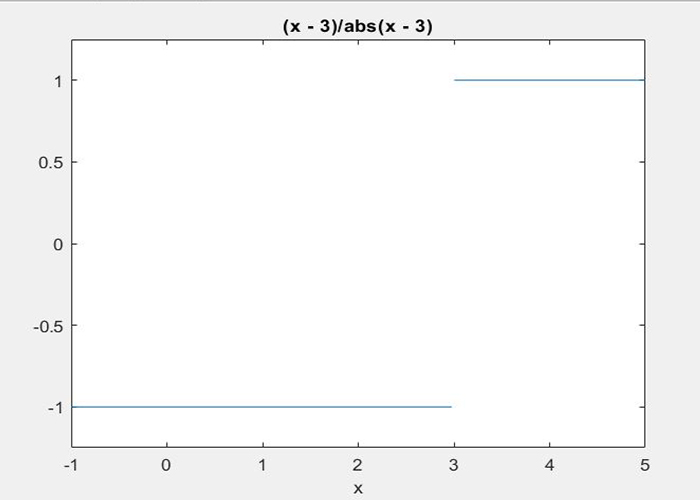
ممکن است یک تابع در نقطه‌ای حد نداشته باشد،‌ اما حد چپ و یا حد راست در آن نقطه داشته باشد. این اتفاقات معمولا در نقاط گسستگی تابع رخ می‌دهد. برای نشان دادن این موضوع با معرفی یک تابع،‌ ابتدا با متلب و دستور limit حد چپ و راست آن را به صورت جداگانه محاسبه می‌کنیم (که چون با هم برابر نیستند تابع در آن نقطه حد ندارد) و سپس با رسم نمودار این مفاهیم را روشن‌تر خواهیم دید. تابع زیر را در نظر بگیرید:

$ f(x) = \frac{x-3}{\left | x-3 \right |} $

این تابع در نقطه‌ی صفر حد ندارد. زیرا حد راست آن ۱ و حد چپ آن ۱- است. کد زیر را در یک فایل اسکریپت اجرا کنید: (در تابع limits ابتدا خود تابع f، سپس متغیر مورد نظر، سپس عددی که باید حد در آن حساب شود و در نهایت عبارات ‘rigth’ و ‘left’ به ترتیب برای حد‌های راست و چپ،‌ به عنوان آرگومان‌ها ورودی داده می‌شوند.)

syms x
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])

limit(f,x,3)
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

syms x

f = (x - 3)/abs(x-3);

ezplot(f,[-1,5])

limit(f,x,3)

l = limit(f,x,3,'left')

r = limit(f,x,3,'right')

با اجرای کد بالا تصویر و خروجی آن را به شکل زیر مشاهده می‌کنید:

ans =
NaN
 
l =
-1
 
r =
1

ans =

NaN

l =

-1

r =

تمرین برنامه نویسی

بررسی قوانین مشتق در متلب

بگذارید به طور خلاصه معادلات یا قوانین مختلفی را برای مشتق توابع بیان کرده و این قوانین را با مشتق در متلب ارزیابی کنیم. برای این منظور، برای مشتق مرتبه اول f ‘(x) و برای مشتق مرتبه دوم f “(x) خواهیم نوشت. در زیر قوانین مشتق ذکر شده است:

قانون ۱: برای هر تابع f و g و هر عدد واقعی a و b مشتق توابع زیر موجودند:

$ h(x) = af(x) + bg(x) $
$ h'(x) = af'(x) + bg'(x) $

قانون ۲: قوانین جمع و تفریق بیان می‌کنند که اگر f و g دو تابع باشند، به ترتیب داریم:

$(f + g)’ = f’ + g’$

$(f – g)’ = f’ – g’$

قانون ۳: قانون شرکت پذیری بیان می‌کند که اگر f و g دو تابع باشند، داریم:

$ (f.g)’ = f’.g + g’.f $

قانون ۴: قانون ضریب بیان می‌کند که اگر f و g دو تابع باشند:

$ (\frac{f}{g})’ = \frac{(f’.g – g’.f)}{g^2} $

قانون ۵: قانون چندجمله‌ای یا قدرت ابتدایی بیان می‌کند:

اگر $y = f (x) = x^n $، آنگاه $f’ = n. x^{n-1} $

نتیجه مستقیم این قاعده این است که مشتق عدد ثابت صفر است.

قانون ۶:قانون زنجیره‌ای بیان می‌کند که مشتق تابع h(x) = f(g(x)) به صورت زیر است:

$h'(x) = f'(g (x)). g ‘(x) $

مثال در متلب: یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ کنید. در این قطعه کد به ترتیب همه‌ی قوانین را با متلب بررسی می‌کنیم.

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

syms x

syms t

f = (x + 2)*(x^2 + 3)

der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)

der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)

der4 = diff(f)

f = (x^2 + 1)^17

der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)

der6 = diff(f)

با اجرای فایل، متلب نتیجه زیر را نمایش می‌دهد:

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

f =

(x^2 + 3)*(x + 2)

der1 =

2*x*(x + 2) + x^2 + 3

f =

(t^(1/2) + t^3)*(t^2 + 3)

der2 =

(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)

f =

(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 =

(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)

f =

(2*x^2 + 3*x)/(x^3 + 1)

der4 =

(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2

f =

(x^2 + 1)^17

der5 =

34*x*(x^2 + 1)^16

f =

1/(t^3 + 3*t^2 + 5*t - 9)^6

der6 =

-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

تمرین برنامه نویسی

مشتقات توابع نمایی، لگاریتمی و مثلثاتی

در ادامه‌ برای نشان دادن کاربردهای عملی مشتق در متلب چند نمونه از مشتق‌های معروف توابع نمایی،‌ لگاریتمی و مثلثاتی را به همراه پیاده‌سازی ‌‌آن‌ها در متلب قرار داده‌ایم.

تابع	مشتق
$c^{a.x}$	$c^{a.x}.a.lnc$
e^x	e^x
lnx	$ ۱/x $
x^x	$x^x.(1 + ln x)$
sin(x)	cos(x)
cos(x)	sin(x)-
tan(x)	۱ + tan^2(x)
cot(x)	$ ۱ + cot^2(x) $
sec(x)	sec(x).tan(x)
csc(x)	csc(x).cot(x)-

مثال: یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ کنید. در ادامه به بررسی برخی از این مثال‌ها در متلب می‌پردازیم.

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

syms x

y = exp(x)

diff(y)

y = x^9

diff(y)

y = sin(x)

diff(y)

y = tan(x)

diff(y)

y = cos(x)

diff(y)

y = log(x)

diff(y)

y = log10(x)

diff(y)

y = sin(x)^2

diff(y)

y = cos(3*x^2 + 2*x + 1)

diff(y)

y = exp(x)/sin(x)

diff(y)

با اجرای فایل، متلب نتیجه زیر را نمایش می‌دهد:

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

y =

exp(x)

ans =

exp(x)

y =

x^9

ans =

9*x^8

y =

sin(x)

ans =

cos(x)

y =

tan(x)

ans =

tan(x)^2 + 1

y =

cos(x)

ans =

-sin(x)

y =

log(x)

ans =

1/x

y =

log(x)/log(10)

ans =

1/(x*log(10))

y =

sin(x)^2

ans =

2*cos(x)*sin(x)

y =

cos(3*x^2 + 2*x + 1)

ans =

-sin(3*x^2 + 2*x + 1)*(6*x + 2)

y =

exp(x)/sin(x)

ans =

exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

محاسبه مشتقات مرتبه بالاتر

برای محاسبه مشتقات بالاتر یک تابع f، از سینتکس diff(f,n) استفاده می‌کنیم. اجازه دهید مشتق دوم تابع $ y = f(x) = x .e^{-3x} $ را محاسبه کنیم:

f = x*exp(-3*x);
diff(f, 2)

1 2	f = xexp(-3x); diff(f, 2)

متلب کد را اجرا می‌کند و نتیجه زیر را برمی‌گرداند:

ans =

9*x*exp(-3*x) - 6*exp(-3*x)

ans =

9*x*exp(-3*x) - 6*exp(-3*x)

مثال: بیایید یک مسئله حل کنیم. با توجه به تابع y = f (x) = 3 sin (x) + 7 cos (5x). ما باید دریابیم که آیا معادله f “+ f = -5cos (2x) درست است یا خیر.

یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ کنید:

syms x
y = 3*sin(x)+7*cos(5*x);
lhs = diff(y,2)+y;        %بخش چپ معادله
rhs = -5*cos(2*x);        %بخش راست معادله
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

syms x

y = 3*sin(x)+7*cos(5*x);

lhs = diff(y,2)+y; %بخش چپ معادله

rhs = -5*cos(2*x); %بخش راست معادله

if(isequal(lhs,rhs))

disp('Yes, the equation holds true');

else

disp('No, the equation does not hold true');

end

disp('Value of LHS is: '), disp(lhs);

وقتی فایل را اجرا می‌کنید، بخش چپ و راست معادله با هم مقایسه می‌شود (می‌توانید به بخش عبارات شرطی در متلب مراجعه کنید) و نتیجه زیر نمایش داده می‌شود:

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

No, the equation does not hold true

Value of LHS is:

-168*cos(5*x)

یافتن ماکسیمم و مینیمم‌های یک منحنی

اگر ما به دنبال حداکثرها و حداقل‌های محلی برای یک نمودار هستیم، اساسا به دنبال بالاترین یا پایین‌ترین نقاط نمودار تابع در یک مکان خاص یا طیف خاصی از مقادیر دامنه هستیم.

برای یک تابع y = f (x) به نقاط موجود در نمودار که نمودار دارای شیب صفر است، نقاط بحرانی گفته می‌شود. به عبارت دیگر نقاط بحرانی جایی هستند که f ‘(x) = 0 باشد (تعریف دقیق نقاط بحرانی، نقاطی هستند که در نمودار مقدار دارند و مشتق آن‌ها یا صفر است و یا وجود ندارد). برای یافتن نقاط اکسترمم (مینیمم یا ماکسیمم) تابع، باید مشتق را برابر صفر قرار دهیم و معادله را حل کنیم.

مثال: تابع f (x) = 2x^3 + 3x^2 – 12x + 17 را در نظر بگیرید. می‌خواهیم طی ۳ مرحله در بازه‌ی منفی ۶ تا ۶، نقاط مینیمم و ماکسیمم آن را پیدا کنیم.

مرحله اول: تابع را وارد کرده و نمودار آن را رسم کنیم.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;
ezplot(y)

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17;

ezplot(y)

هدف ما یافتن مقادیر حداقل و حداکثر محلی روی نمودار است، بنابراین اجازه دهید حداکثر و حداقل‌های محلی را برای فاصله [۶ ، ۶-] روی نمودار پیدا کنیم. به نمودار توجه کنید:

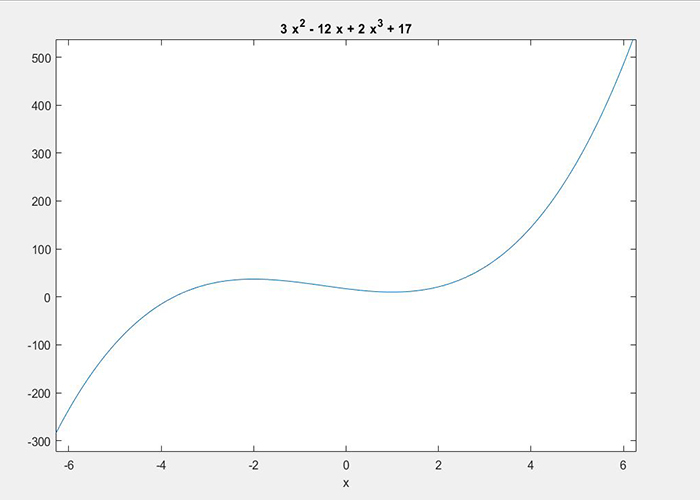
مرحله‌ی دوم: مشتق را محاسبه می‌کنیم:

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = diff(y)

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = diff(y)

متلب کد را اجرا می‌کند و نتیجه زیر را برمی‌گرداند:

g =

   6*x^2 + 6*x - 12

g =

6*x^2 + 6*x - 12

مرحله سوم: در این مرحله باید ببینیم در چه مقادیری در بازه مورد نظر، مشتق تابع برابر با صفر است. اجازه دهید تابع مشتق یا همان g را حل کنیم تا مقادیر را به صفر برسانیم.

syms x y
= 2*x^3 + 3*x^2 - 12*x + 17;
g = diff(y);

s = solve(g)

syms x y

= 2*x^3 + 3*x^2 - 12*x + 17;

g = diff(y);

s = solve(g)

متلب کد را اجرا می‌کند و نتیجه زیر را برمی‌گرداند:

s =
   1
   -2

s =

-2

این نتایج با ظاهر نمودار ما همخوانی دارد. بنابراین اجازه دهید تابع f را در نقاط بحرانی x = 1 ، -۲ ارزیابی کنیم. با استفاده از دستور subs می‌توان خروجی یک تابع را به ازای یک مقدار در ورودی محاسبه کرد. در نهایت همه‌ی کدهای بالا به صورت زیر خلاصه می‌شود:

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;

% رسم نمودار
ezplot(y)

%گرفتن مشتق
g = diff(y);

%محاسبه‌ی ریشه‌های مشتق
s = solve(g);

%محاسبه‌ی مقادیر تابع در ریشه‌های مشتق، که همان مقادیر اکسترمم هستند
subs(y, 1), subs(y, -2)

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17;

% رسم نمودار

ezplot(y)

%گرفتن مشتق

g = diff(y);

%محاسبه‌ی ریشه‌های مشتق

s = solve(g);

%محاسبه‌ی مقادیر تابع در ریشه‌های مشتق، که همان مقادیر اکسترمم هستند

subs(y, 1), subs(y, -2)

متلب کد را اجرا می‌کند و نتیجه نهایی که همان مینیمم و ماکسیمم‌های محلی تابع در بازه‌ی منفی تا مثبت ۶ هستند را برمی‌گرداند:

ans =
   10
ans =
   37

ans =

تمرین برنامه نویسی

حل معادلات دیفرانسیل در متلب

MATLAB دستور dsolve را برای حل معادلات دیفرانسیل به صورت نمادین فراهم می‌کند. اساسی ترین شکل دستور dsolve برای یافتن راه حل برای یک معادله واحد است. به مثال زیر توجه کنید: (eqn یک رشته متنی است که همان معادله است)

dsolve('eqn')

1	dsolve('eqn')

شما همچنین می‌توانید شرایط اولیه و مرزی را برای این معادله تعیین کنید. به سینتکس زیر توجه کنید:

dsolve('eqn','cond1', 'cond2',…)

1	dsolve('eqn','cond1', 'cond2',…)

برای استفاده از دستور dsolve، مشتقات با D نشان داده می‌شوند. به عنوان مثال، معادله ای مانند f'(t)=-2*f+cos(t) بصورت زیر وارد می‌شود. مشتقات بالاتر با به توان رسیدن D به ترتیب مشتق در متلب نشان داده می‌شوند. به عنوان مثال معادله f “(x) + 2f ‘(x) = 5sin3x باید به صورت زیر وارد شود:

Df = -2*f + cos(t)

D^2y + 2Dy = 5*sin(3*x)

مثال معادله مرتبه اول و مرتبه دوم

بیایید یک مثال ساده از معادله دیفرانسیل مرتبه اول را داشته باشیم: y ‘= 5y

s = dsolve('Dy = 5*y')

1	s = dsolve('Dy = 5*y')

متلب کد را اجرا می‌کند و نتیجه زیر را برمی‌گرداند: (c1 یا c2 ضرایب ثابت هستند)

s =
   C2*exp(5*t)

1 2	s = C2exp(5t)

بیایید مثال دیگری از معادله دیفرانسیل مرتبه دوم را به همراه شرایط اولیه بررسی کنیم. y”-y = 0 ، y(0) = -1 ، y'(0) = 2

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

1	dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

متلب کد را اجرا می‌کند و نتیجه زیر را برمی‌گرداند:

ans =

   exp(t)/2 - (3*exp(-t))/2

ans =

exp(t)/2 - (3*exp(-t))/2

تمرین برنامه نویسی

سینتکس مشتق و حد در octave

اگر بخواهید در اکتاو از مشتق و حد استفاده کنید،‌ می‌توانید از فرمت زیر استفاده کنید:

pkg load symbolic
symbols

% محاسبه مشتق
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

%محاسبه حد
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

pkg load symbolic

symbols

% محاسبه مشتق

t = sym("t");

f = 3*t^2 + 2*t^(-2);

differentiate(f,t)

%محاسبه حد

x = sym("x");

subs((x^3+5)/(x^4+7),x,0)

با اجرای کد نتیجه به صورت زیر خواهد بود:

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

ans =
   0.7142857142857142857

ans =

-(4.0)*t^(-3.0)+(6.0)*t

ans =

0.7142857142857142857

برچسب‌ها: دوره آموزشی متلب

تیم محتوایی فنولوژی

گروهی از متخصصان حوزه‌های مختلف

مطالب مشابه

بازخورد در متن

دیدن همه دیدگاه‌ها

مشتق در متلب |‌ MATLAB calculus10 دقیقه مطالعه

حسابان در متلب

محاسبه مشتق در متلب

محاسبه حد در متلب

حد چپ و راست در متلب

بررسی قوانین مشتق در متلب

مشتقات توابع نمایی، لگاریتمی و مثلثاتی

محاسبه مشتقات مرتبه بالاتر

یافتن ماکسیمم و مینیمم‌های یک منحنی

حل معادلات دیفرانسیل در متلب

مثال معادله مرتبه اول و مرتبه دوم

سینتکس مشتق و حد در octave

تیم محتوایی فنولوژی

مطالب مشابه

lambda در پایتون | تابع بدون نام در پایتون

تابع در پایتون | ایجاد و استفاده از توابع در پایتون

معادل switch case در پایتون | match case در پایتون

فنولوژی را در شبکه‌های اجتماعی دنبال کنید

©۲۰۲۰ – کلیه حقوق مادی و معنوی متعلق به فنولوژی است.