نمادهای ریاضی از گذشته تا به امروز | آشنایی با انواع نمادهای ریاضی5 دقیقه مطالعه

این نوشته، بخشی از مجموعه‌ای است که به بررسی خلاصه‌وار تحول نمادهای ریاضی از گذشته تا به امروز خواهد پرداخت. مطالب بسیار زیادی از ابتدای کار انسان‌ها با اعداد در هزاران سال پیش تا به امروز وجود دارد. در این مجموعه سعی می‌کنیم به خلاصه‌ی مفید و در عین حال جالبی از آن‌ها اشاره کنیم. در این نوشته از فنولوژی، ابتدا قصد داریم به بررسی اعداد، نمادهای چهار عمل اصلی و تساوی بپردازیم. در ادامه به نمادهای مفاهیم پیشرفته‌تر ریاضی، از جمله توان، رادیکال، نامساوی، هم‌نهشتی و … خواهیم پرداخت.

چرا نیاز به وجود نمادهای ریاضی احساس شد؟

جواب دادن به این سوال کار سختی نیست. ریاضیات، علمی است که عمدتا با اعداد سروکار دارد. وقتی که نوشتار به وجود آمده است، مسلما از اولین مواردی که بعدها به آن فکر شده این بوده که اعداد هم نوشته‌ شوند. حال واضح است که قبل از هر چیز باید مشخص می‌شد که اعداد چگونه نوشته شوند.

نمادهای ریاضی که برای نمایش اعداد استفاده می‌شده است، در تمدن‌های مختلف، گوناگون بوده است. حتی دستگاه‌های عددنویسی و در نتیجه تعداد نمادهایی که برای ساخت همه‌ی اعداد در آن‌ دستگاه عددنویسی لازم است، متفاوت بوده‌اند. در مورد دستگاه‌های عددنویسی مختلف نیز می‌توان بسیار بحث کرد. از آنجا که مثال‎‌های بسیاری از نمادهایی که برای اعداد در تمدن‌های مختلف به‌کار می‌رفته وجود دارد، در اینجا به آن‌ها نمی‌پردازیم. با جستجوی نام هر تمدن می‌توانید نمادهایی که استفاده‌ می‌کردند را ببینید.

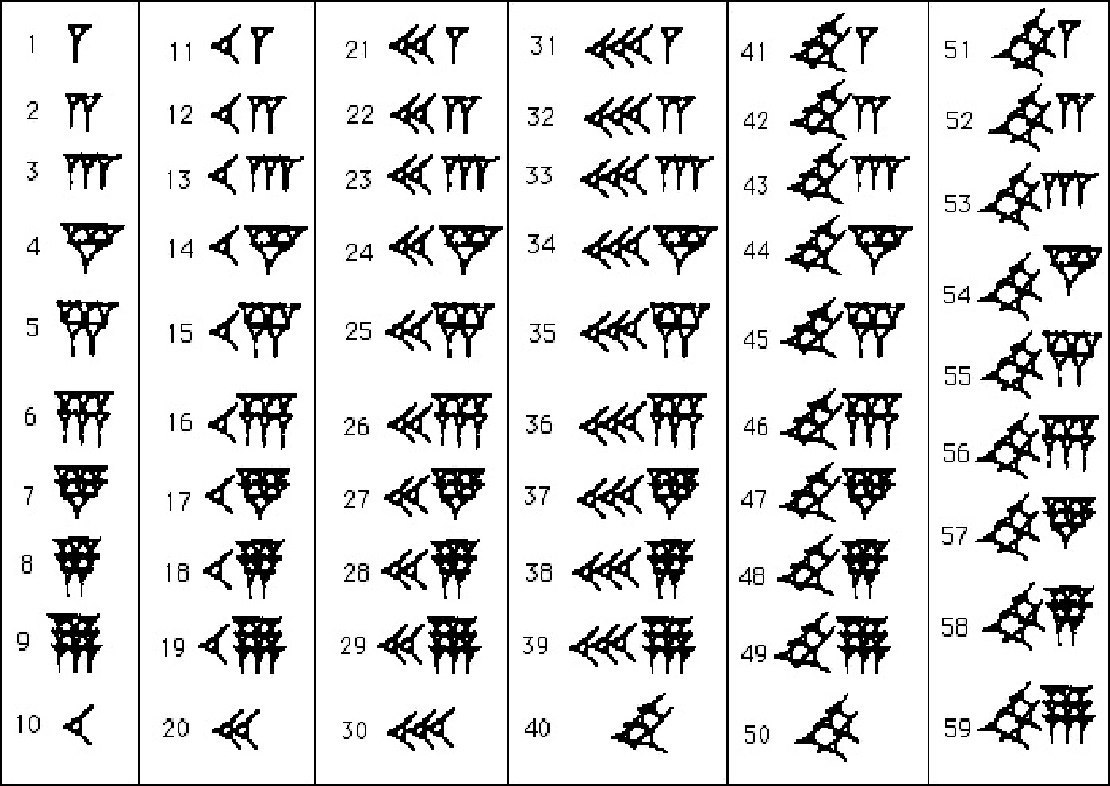
تصویری که در ابتدای این نوشته می‌بینید، نمادهایی است که بابلیان باستان استفاده می‌کردند. برای اعداد بیش‌تر از ۵۹ نماد وجود ندارد؛ چون آن‌ها از دستگاه عددنویسی‌ای با مبنای ۶۰ استفاده‌ می‌کردند که هنوز هم در محاسبات مربوط به زمان کاربرد دارد.

بعد از تعیین نمادهایی برای اعداد، نوبت به تعیین نمادهایی برای موجودات دیگر در ریاضیات مثل عمل‌ها می‌رسد. البته در زمان‌های قدیم، مفاهیم ریاضی زیادی مانند امروز وجود نداشت که لازم باشد برای هرکدام نمادی تعیین شود. از مهم‌‌ترین موجوداتی که نیاز به نماد داشتند می‌توان به چهار عمل اصلی حساب اشاره کرد.

نمادهای ریاضی جمع و تفریق

جمع و تفریق از اولین عمل‌هایی بودند که مفهوم آن‌ها برای تمدن‌های قدیمی واضح بود. نمادهای ریاضی که برای نمایش این عمل‌ها استفاده می‌شد در تمدن‌های قدیمی متفاوت بوده است؛ مثلا مصریان باستان نمادهایی شبیه به پاهای یک انسان را به کار می‌بردند. در این تصویر می‌‌توانید این نمادها را مشاهده کنید. نماد سمت چپ برای جمع، و دیگری برای تفریق به کار می‌رفته است.

در قرن ۱۴ و ۱۵ میلادی، شاهد آغاز کار با نمادهای جمع و تفریقی که ما امروزه استفاده می‌کنیم، هستیم. نخستین باری که علامت جمع به شکل امروزی ظاهر شده است، به اواسط قرن ۱۴ میلادی برمی‌گردد که ریاضی‌دانی فرانسوی به نام «Nicole Oresme» آن را به‌کار برده است. او در کتاب «Algorismus Proportionum» این علامت را به‌ عنوان کوتاه‌شده‌ی «et» به کار می‌برد که کلمه‌ای لاتین به معنای «and» است و در واقع بیان‌گر همان مفهوم جمع بوده‌است.

علامت تفریق به شکل امروزی هم اولین بار توسط ریاضی‌دانی آلمانی به نام «Johannes Widmann» در سال ۱۴۸۹ میلادی به کار رفت. نخستین باری که علامت امروزی جمع و تفریق چاپ شدند، در کتابی از همین ریاضی‌دان به نام «Mercantile Arithmetic» بود که تصویر زیر مربوط به آن است.

با وجود اینکه علامت‌های بالا ابداع شده بودند اما مدتی کوتاه طول کشید تا رایج شوند؛ مثلا اروپایی ها از «P» و «M» نیز برای نشان دادن جمع و تفریق استفاده می‌کردند که حروف ابتدایی کلمات «Plus» و «Minus» هستند. با گذشت زمان کوتاهی، استفاده از علامت‌های امروزی مخصوصا توسط آلمانی‌ها بیشتر شد و بعدها همگان از آن‌ها استفاده کردند.

نمادهای ریاضی ضرب و تقسیم

معمولا تمدن‌ها قدیمی از جمله یونان و چین باستان نماد خاصی برای نشان دادن مفهوم ضرب و تقسیم نداشتند و از کلمات برای نشان دادن آن‌ها استفاده می‌کردند. جلوتر از آن‌ها ریاضی‌دان‌های قرن ۱۵ میلادی در اروپا از علامت‌های «M» و «D» برای ضرب و تقسیم استفاده می‌کردند که حروف ابتدایی کلمات ضرب و تقسیم اند.

نماد ریاضی «$\times$» برای ضرب، اولین بار توسط ریاضی‌دانی انگلیسی به نام «William Oughtred» استفاده شد. این ریاضی‌دان از حدود ۱۵۰ نماد در نوشته‌های خود استفاده کرده که قبل از او استفاده نشده بودند؛ البته تعداد بسیار کمی از آن‌ها امروزه استفاده می‌شوند. در آن زمان هم لایبنیز با این نماد برای ضرب مخالف بود. او در سال ۱۶۹۸ در نامه‌ای که برای یوهان برنولی فرستاده بود، نوشته بود که «من از این نماد برای نشان دادن ضرب خوشم نمی‌آید چون به راحتی با ‘x’ اشتباه می‌شود». پیشنهاد لایبنیز برای ضرب، نماد ‘.’ ، یعنی همان نقطه بود. همچنین برای نمایش کسرها و تقسیم دو عدد، به‌جای یک نقطه از دو نقطه استفاده می‌کرد. نماد ‘:’ برای تقسیم، پیش‌تر نیز در نوشته‌های لایبنیز موجود بود و لایبنیز از سال ۱۶۸۴ آن را در نوشته‌هایش استفاده می‌کرده است. البته نماد ‘:’ برای نمایش کسرها، قبل‌تر نیز مرسوم بوده است (سال ۱۶۳۳ در کتابی به نام «Johnson Arithmetik» استفاده شده است).

یکی دیگر از نمادهای ریاضی که امروزه برای ضرب رایج است، نماد ‘*’ است که بیشتر در موضوعات مربوط به کامپیوتر می‌بینیم. این نماد را «Johann Rahn» در سال ۱۶۵۹ در «Teutsche Algebra» استفاده کرده است. نماد «$\div $» نیز نخستین بار در همین کتاب به عنوان نماد تقسیم استفاده شده است.

ریاضی‌دانی به نام «Michael Stifel» نیز از نماد ‘(‘ نیز برای نمایش کسرها استفاده‌ کرده است؛ مثلا ۲۴(۸ که همان ${\frac{24}{8}}$ است؛ البته این نماد برای انجام عمل تقسیم استفاده نمی‌شده است.

یکی دیگر از نمادهایی که هنوز برای نمایش کسرها و انجام عمل تقسیم استفاده می‌شود، نماد ‘/’ است. این نماد را «Thomas Twining» در سال ۱۷۱۸ استفاده کرده است که بسیار مشابه با خط افقی است که مسلمانان در قرن ۱۲ برای نمایش کسرها ابداع کرده بودند.

به عنوان آخرین نمونه‌ی تقسیم نیز به نماد تقسیم تفصیلی (Long division) اشاره می‌کنیم. منظور از تقسیم تفصیلی همان تقسیمی است که در آن تک‌تک مراحل را ذکر می‌کنیم تا خارج قسمت و باقی‌مانده تعیین شوند. در اولین تصویر از مجموعه‌ی زیر می‌بینیم که تقسیم تفصیلی به‌صورت $ \left. 7 \right ) 12096 \left ( 1728 \right. $ نوشته شده است که اعداد نوشته شده از چپ به راست به‌ترتیب، همان مقسوم‌علیه، مقسوم و خارج‌قسمت هستند. نمادهای دیگر برای تقسیم تفصیلی را در تصاویر دیگر مشاهده می‌کنید.

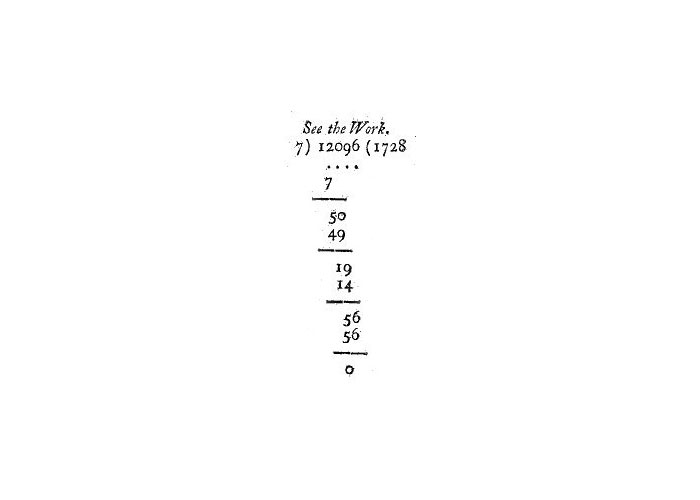
روند نزدیک شدن نماد تقسیم تفصیلی در گذشته، به نمادی که ما امروزه استفاده می کنیم، در تصاویر بالا واضح است. اما در هیچ کتاب تاریخ ریاضیات، تاریخ دقیقی برای ابداع نماد امروزی تقسیم تفصیلی ذکر نشده است؛ یکی از دلایل این امر این است که نماد امروزی که استفاده می‌کنیم، به تدریج و با گذشت زمان جا افتاده است.

نماد تساوی در ریاضیات

تا قبل از قرن ۱۶ میلادی در اغلب کشورها مفهوم تساوی با کلمه‌ی «تساوی» در آن زبان نشان داده می‌شد. در سال ۱۵۵۷، ریاضی‌دانی ولزی به نام «Robert Recorde» نماد ‘=’ را در کتاب «The Whetsone of Witte» برای تساوی به‎‌کار برد. همچنین نخستین بار در همین زمان بود که نمادهای ‘+’ و ‘-‘ در یک نوشته به زبان انگلیسی استفاده شدند. در تصویر زیر قسمتی از این کتاب را مشاهده می‌کنید که در آن توضیحاتی برای نماد تساوی ذکر شده است.