قضیهی مقدار میانگین از جمله مهمترین قضایا در مبحث مشتق ریاضی عمومی یک دانشگاه است. در ابتدا شما را دعوت میکنیم که اگر با قضیهی مقدار میانی آشنا نیستید، قبل از خواندن این مقاله، مقالهی قضیه مقدار میانی از فنولوژی را مطالعه کنید؛ زیرا در حل برخی از مثالهایی که در اینجا آوردهایم از از قضیه مقدار میانی استفاده شده است. این سری قضایا با نام قضایای وجودی تلقی میشوند. زیرا به ما اطمینان وجود چیزهای خاصی را میدهند.
صورت قضیه مقدار میانگین
اگر بخواهیم این قضیه را به زبان ریاضیات برای شما بازگو کنیم، به صورت زیر تعریف میکنیم و در ادامه مثالی از آن در زندگی روزمره برایتان میآوریم تا بهتر صورت قضیه مقدار میانگین را فراگیرید:
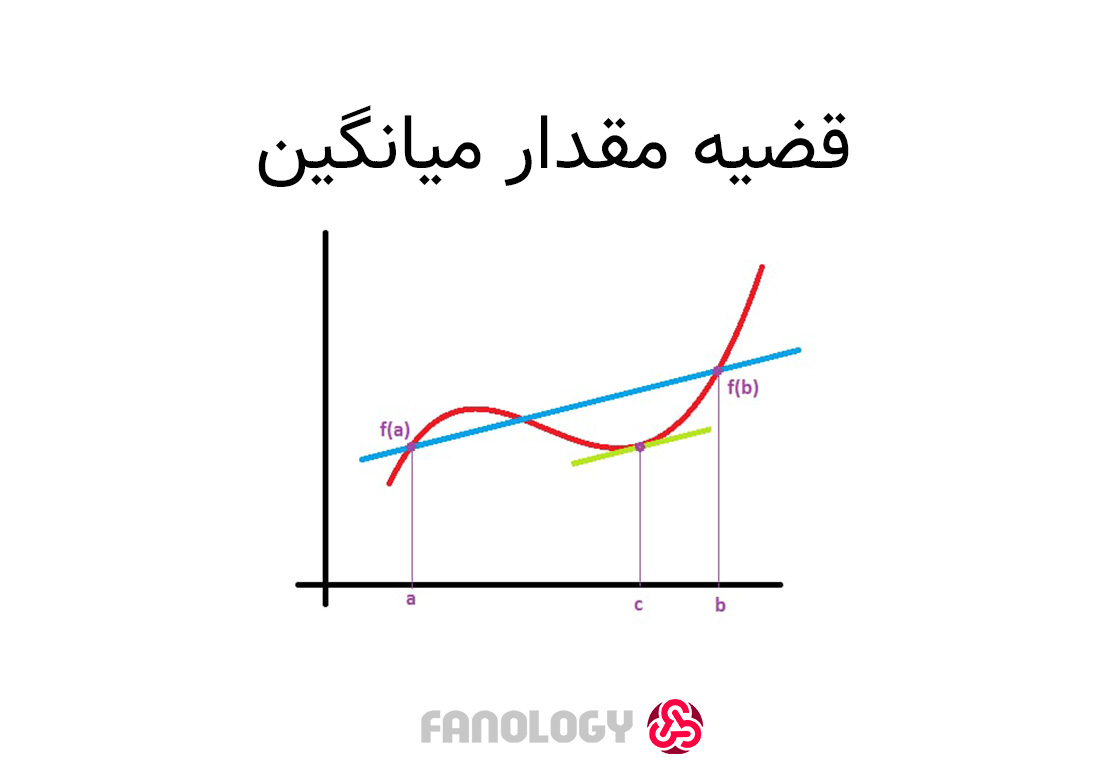
اگر تابع $f(x)$ را تابعی پیوسته بر بازهی $[a,b]$ در نظر بگیریم و این تابع بر بازهی باز $(a,b)$ مشتقپذیر باشد، آنگاه عددی مانند $c$ در بازهی $(a,b)$ یافت میشود به طوریکه داشته باشیم ${f}'(c)=\frac{f(b)-f(a)}{b-a}$.
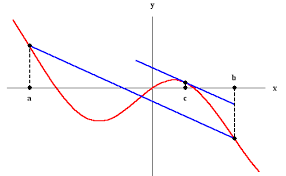
این قضیه به طور صریح به ما میگوید که اگر شیب خط متصل کنندهی نقاط ابتدایی و انتهایی تابعی پیوسته را داشته باشیم، آنگاه میتوان مطمئن بود که مشتق حداقل یک نقطه در آن بازه برابر آن شیب خواهدبود؛ یا به بیانی دیگر خط مماسی بر نمودار وجود دارد که موازی خط اولیهی ما باشد.
صورت کلیتر این قضیه یا همان صورت تعمیم یافتهاش فعلا مورد بحث ما نیست و میخواهیم با استفاده از همین قضیهی به ظاهر ساده، مسائل بسیاری در ریاضیات را حل نماییم و با کاربرد آن در زندگی آشنا شویم. مثالهایی که میآوریم برای همهی افراد، اعم از دانشجویان و دانشآموزان علاقهمند به ریاضیات، قابل استفاده است. با مثالها و تمرینهای نسبتا ساده آغاز میکنیم و با مثالها و تمرینهای به نسبت پیشرفتهتر برای افراد علاقهمند و کسانی که میخواهند خودرا برای امتحانات آماده کنند، مقاله را به پایان میبریم. قبل از دیدن پاسخ هر مثال حل شده یا راهنمایی تمرینها، حتما حداقل به مقدار ۳۰ دقیقه روی آن مسئله فکر کنید تا از ریاضیات، بیشتر لذت ببرید. با ما همراه باشید….
مثالهایی از قضیهی مقدار میانگین
مثال۱ – قضیه مقدار میانگین در کیلومتر شمار ماشین
فرض کنید در حال سفر از استان اصفهان به استان تهران هستید. پس از پنج ساعت طاقت فرسا در ماشین شخصیتان، بالاخره به مقصدتان یعنی تهران میرسید. نگاهی به کیلومترشمار میاندازید و متوجه میشوید که در این مدت پنج ساعت، مسافت ۴۳۵ کیلومتر را طی کردهاید. از قوانین فیزیک میدانیم که مقدار سرعت متوسط ما در مسیری به مسافت $x$ که در مدت زمان $t$ طی کردیم، برابر $\bar{v}=\frac{ x}{ t}$ خواهد بود. حال، شاید کنجکاو شوید و بخواهید دربارهی محدودهی سرعتی که در این مدت با آن رانندگی میکردید، اطلاعات کسب کنید.

شما در این حال مقدار سرعت متوسط را محاسبه میکنید و به مقدار $\frac{435}{5}=87km/h$ میرسید. حال، یکی از نتایج قطعی که از این مقدار به دست آمده، این است که حتما در مسیرتان، لااقل یک بار با این سرعت در حرکت بودهاید؛ به بیانی دیگر لحظهای در مسیر وجود داشته است که عقربهی نشاندهندهی سرعت ماشین روی عدد $۸۷km/h$ بوده است.
اثبات این ادعا به راحتی صورت میگیرد؛ چرا که اگر همواره سرعت بیشتر از ۸۷ باشد آنگاه سرعت متوسط ما ۸۷ نخواهد بود(چرا؟) و برای کمتر از ۸۷ نیز استدلالی مشابه داریم. حال فرض میکنیم در لحظهای این مقدار کمتر از ۸۷ و در لحظه ای دیگر بیشتر از ۸۷ باشد. چون مسیر ما، مسیری پیوسته است و ما در آن توقفی نداشته ایم، پس در هر لحظهی آن دارای سرعت مشخصی هستیم و به همین دلیل نمودار نوسان سرعت پیوسته است. طبق قضیهی مقدارمیانی میتوانیم نتیجه بگیریم که لحظهای بین آن دو لحظه که سرعت کمتر از ۸۷ و بیشتر ۸۷ بود، وجود دارد که سرعت در آن لحظه دقیقا ۸۷ باشد.
مثال۲ – قضیه مقدار میانگین در یافتن صفرهای تابع
فرض کنید تابع $f(x)$ بر بازهی $I$ مشتق پذیر باشد و در $n\geq 2$ نقطهی متمایز $I$ صفر شود. ثابت کنید که تابع ${f}'(x)$ باید دستکم در n-1 نقطه از $I$ صفر گردد.
راه حل:
فرض کنید n نقطهای که تابع $f$ در آنها صفر شده است، نقاط $x_{1}< x_{2}< …< x_{n}$ باشند. حال طبق فرض مسئله میدانیم که $f(x_{1})=f(x_{2})=…=f(x_{n})=0$ و اگر ثابت کنیم بین هر دو $x_{i}$ متوالی که $i=1,2,…,n$ است، وجود دارد عددی مانند $c$ به طوریکه ${f}'(c)=0$ آنگاه حکم مسئله ثابت شده است(چرا؟).
حال میآییم شیب خط واصل بین هردو نقطهی صفر کنندهی تابع را حساب میکنیم:
$m=\frac{f(x_{i+1})-f(x_{i})}{x_{i+1}-x_{i}}=\frac{0-0}{x_{i+1}-x_{i}}=0$
سپس طبق قضیه مقدار میانگین میتوان نتیجه گرفت که بین هر دو $x_{i}$ متوالی که $i=1,2,…,n$ است، وجود دارد عددی مانند $c$ به طوریکه ${f}'(c)=0$ که معادل حکمی است که در بالا به دست آوردیم.
تمرین۱
فرض کنید $f:\mathbb{R}\rightarrow \mathbb{R}$ بینهایت بار مشتقپذیر باشد و برای عدد طبیعی $n$ داشته باشیم:
$f(1)=f(0)={f}'(0)={f}”(0)=…=f^{(n)}(0)=0$
که در آن، عبارت $f^{(n)}(x)$ به معنای مشتق n-ام تابع $f(x)$ است. ثابت کنید $x\in (0,1)$ وجود دارد به طوریکه $f^{(n+1)}(x)=0$.
راهنمایی:
سعی کنید با استفاده از مثال قبلی و قضیه مقدار میانگین، در بازهی $(۰,۱)$ عددی مانند $c$ بیابید که ${f}'(c)=0$ و همین طور این کار را در بازهی جدید $(۰,c)$ انجام دهید و این کار را آنقدر ادامه دهید تا به حکم مسئله برسید.
مثال۳ – قضیه مقدار میانگین در یافتن تعداد جوابهای معادلات
ثابت کنید معادلهی $cos(sinx)=x$ دقیقا یک جواب حقیقی دارد.
راه حل:
ما اگر کمی به معادلهای که داده شده توجه کنیم، در مییابیم که با یک تساوی تابعی روبهرو هستیم. توابع $f(x)=x$ و $g(x)=cos(sinx)$. حال اگر تابع جدیدی مانند $h(x)$ از تفاضل این دو بسازیم و بگوییم دقیقا یک ریشه خواهد داشت، حکم مسئله را برآورده کردهایم. پس تابعی مانند $h(x)=x-cos(sinx)$ را ساخته و مسئله را روی آن بررسی میکنیم.
دقت کنید که همواره داریم $-۱\leq cosx\leq 1$. پس یعنی به ازای $\left | x \right |> 1$ خواهیم داشت $h(x)\neq 0$ (چرا؟).پس برای $-۱\leq x\leq 1$ اگر ثابت کنیم که $h$ تنها دارای یک ریشه است، درواقع به حکم مسئله رسیدهایم.
با برهان خلف میخواهیم مسئله را پیش ببریم. یعنی فرض کنیم که $h$ دارای حداقل دو ریشه میباشد؛ و این طبق قضیهی مقدار میانگین به این معناست که $c$ در $[-۱,۱]$ وجود دارد به طوریکه ${h}'(c)=0$. حالا مشتق تابع را به دست میآوریم تا ببینیم اگر بخواهد این اتفاق بیافتد، به چه نتایجی میرسیم.
$h(x)=x-cos(sinx)\Rightarrow {h}'(x)=1+cosx.sin(sinx)$
طبق نتیجهای که در بالا گرفتیم، باید داشته باشیم ${h}'(c)=1+cosc.sin(sinc)=0$. داریم:
$cosc.sin(sinc)=-1\Rightarrow \left | cosc.sin(sinc) \right |=\left | -1 \right |=1$
و این یعنی:
$\left | cosc \right |.\left | sin(sinc) \right |=1$
و چون طبق خواص توابع سینوس و کسینوس داریم که $-۱\leq cosx\leq 1$ و $-۱\leq sinx\leq 1$ در نتیجه، طبق تساوی بالا باید حتما داشته باشیم $\left | cosc \right |=\left | sin(sinc) \right |=1$ (چرا؟). این موضوع نتیجه میدهد که طبق $c\in [-1,1]$ باید برای $\left | cosc \right |=1$ داشته باشیم $c=0$ که اگر آن را در عبارت $sin(sinc)$ قرار دهیم، برابر ۱ نخواهد بود و تساوی حاصل در بالا را برآورده نمیکند و این یعنی به تناقض رسیدن فرض اولیهمان که همان بیش از یک ریشه داشتن تابع $h$ بود. در نتیجه تابع حداکثر یک ریشه میتواند داشته باشد. حال با اعمال قضیهی مقدار میانی بر روی تابع $h(x)=x-cos(sinx)$ به راحتی میتوانید ثابت کنید که آن ریشه موجود است که این را به خود شما واگذار میکنیم.
تمرین۲
فرض کنید تابع $f(x)$ بر $[۰,۱]$ پیوسته باشد و در $(۰,۱)$ مشتقپذیر باشد. ثابت کنید $c\in (0,1)$ وجود دارد به طوریکه $c^{2}{f}'(c)+2cf(c)=f(1)$.
راهنمایی:
این سوال، سوال ساده ای نیست و ایده ای نسبتا خفن میخواهد. ما قبلا برای تساویهای تابعی، تابعی جدید از تفاضل آنها میساختیم. اینجا هم در واقع همان کار را میکنیم ولی با یک تفاوت که فرض میکنیم آن تابع جدید، خودش مشتق تابعی دیگر است یعنی تابع را اینگونه در نظر بگیرید ${g}'(x)=x^{2}{f}'(x)+2xf(x)-f(1)$ و سپس از دو طرف معادله اگر انتگرال بگیرید، به دست میآید که $g(x)=x^{2}f(x)-xf(1)$ و با به دست آوردن $g(0)$ و $g(1)$ و قضیه مقدار میانگین در مییابید که $c$ وجود دارد که ${g}'(c)=0$ که همان حکم مسئله میباشد.
تمرین۳
فرض کنید تابع $f$ به گونهای است که روی $[a,b]$ پیوسته است و روی بازهی $(a,b)$ مشتق دوم داشته باشد. پارهخط واصل بین نقاط $(a,f(a))$ و $(b,f(b))$ نمودار تابع را در نقطهی سومی مانند $(c,f(c))$ قطع میکند که $c\in (a,b)$. ثابت کنید نقطهی $t$ در بازهی $(a,b)$ وجود دارد به طوریکه ${f}”(t)=0$.
راهنمایی:
سعی کنید در دو مرحله، از قضیه مقدار میانگین بهره ببرید. در مرحلهی اول بین $a$ و $c$ و بین $b$ و $c$؛ و در مرحلهی دوم بین دو عدد بدست آمده در مرحلهی اول از قضیه مقدار میانگین به حکم مسئله برسید.
تمرین۴
فرض کنید تابع $f(x)$ بر روی بازهی $[-۱,۱]$ پیوسته و بر بازهی $(-۱,۱)$ مشتقپذیر باشد. به ازای هر $x$ در $(-۱,۱)$ داریم ${f}'(x)\leq 1$. اگر $f(1)=1$ و $f(-1)=-1$ آنگاه ثابت کنید $f(0)=0$.
راهنمایی:
بهترین راه حل برای این سوال، برهان خلف است. فرض کنید $f(0)\neq 0$ و مسئله را در دو حالت $f(0)> 0$ و $f(0)< 0$ با توجه به قضیهی مقدار میانگین، یک بار بین ۰ و ۱ و یک بار هم بین ۰ و ۱- و با توجه به ${f}'(x)\leq 1$ به تناقض برسید و حکم مسئله را نتیجه بگیرید.
تمرین۵
فرض کنید $f:[0,1]\rightarrow \mathbb{R}$ تابعی پیوسته و ناصفر و روی $(۰,۱)$ مشتقپذیر باشد. اگر $f(0)=1$ و $f(1)=2$ باشد، ثابت کنید $f(x)^{2}-2{f}'(x)$ دارای ریشه است.
راهنمایی:
اگر $f(x)^{2}-2{f}'(x)=0$ قرار دهید، آنگاه با کمی بازی با این معادله میتوان به نتیجهی $\frac{1}{2}=\frac{{f}'(x)}{f(x)^{2}}$ رسید و این مارا به یاد مشتق تابع $\frac{1}{f}$ میاندازد. اگر $g=\frac{1}{f}$ در نظر بگیرید و $g(0)$ و $g(1)$ را به دست آورید، با کمک قضیه مقدار میانگین میتوانید حکم مسئله را نتیجه بگیرید.
Superior essay authors https://www.affordable-papers.net/ will always give their best for composing essays to their pupils.





سلام٫ بسیار ممنون از مثالهایی که بطور کامل حل میکنید چراکه برای تفهیم قضایا و کاربردشان در حل مسائل بسیار راهگشا و ارزشمندند.لطف کنید حل تمرینات را برعهده خواننده نگذارید که اینکار سبب سرخوردگی و رها کردن درس میشود زیرا وقتی بعداز مدتی فکرکردن درحل مسئله اگر راه بجایی نبریم سرخوردگی پیش میاورد ولی به حلش گه نگاه میکنیم وبا حل خودمان مقایسه میکنیم بهتر یاد میگیریم
با تشکر فراوان از زحماتی که برای نشر و رواج ریاضیات متحمل میشوید🌹
منم با این حرف به شدت موافقم