در این قسمت از دوره رایگان آموزش متلب فنولوژی، در مورد انواع تبدیلات مهم مهندسی در متلب، بعنی تبدیل فوریه در متلب و تبدیل لاپلاس در متلب صحبت میکنیم. با ما همراه باشید.
انواع تبدیل در متب
تبدیلات مهم مانند لاپلاس و فوریه برای کاربردهای علمی و مهندسی ایجاد شدهاند. برای مثال با استفاده از تبدیل فوریه در متلب میتوانیم یک سیگنال حوزه زمان را به یک سیگنال حوزه فرکانس منتقل کنیم. و یا با استفاده از تبدیل لاپلاس میتوانیم یک معادله دیفرانیسل را به یک معادله جبری تبدیل کنیم. (محاسبات جبری در متلب)
برای این تبدیلات مهم متلب توابعی دارد که در ادامه به آنها اشاره میکنیم.
تبدیل فوریه در متلب
با استفاده از تبدیل فوریه یک تابع که معمولا از جنس زمان است را به تابعی جدید بدل میکنیم که از جنس f است و معمولا به آن تابع فرکانس یا گستردهی فرکانسی یک سیگنال میگوییم. این متغیر که به آن فرکانس میگوییم، معمولا برحسب هرتز (تعداد تاوبها در واحد زمان) و یا رادیان بر ثانیه بیان میشود.
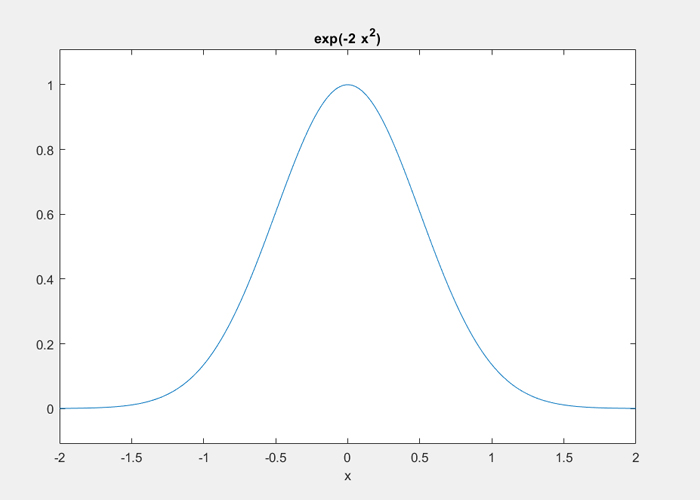
برای تبدیل فوریه در متلب از تابع fourier استفاده میکنیم. به مثال زیر توجه کنید:
|
1 2 3 4 |
syms x f = exp(-2*x^2); %تابع اصلی ezplot(f,[-2,2]) % رسم نمودار تابع FT = fourier(f) % تبدیل فوریه تابع |
متلب کد بالا را اجرا میکند و نتایج زیر را مشاهده خواهید کرد:
کد خروجی:
|
1 2 |
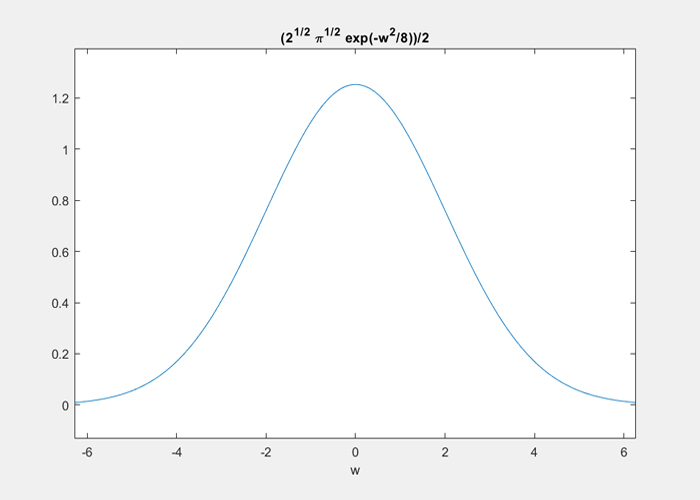
FT = (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2 |
همچنین میتوانید با دستور ezplot(FT) نمودار تبدیل فوریه را نیز به شکل زیر رسم کنید:

معکوس تبدیل فوریه در متلب
با استفاده از تابع ifourier در متلب میتوانید معکوس تبدیل فوریهی یک تابع را محاسبه کنید و آن را از حوزه فرکانس به حوزه زمان برگردانید. به مثال زیر توجه کنید:
|
1 |
f = ifourier(-2*exp(-abs(w))) |
مشاهده خروجی:
|
1 2 |
f = -2/(pi*(x^2 + 1)) |
تبدیل فوریه سریع در متلب | fft
در بسیاری از موارد نیازی به دانستن تبدیل فوریهی دقیق توابع نیست. مخصوصا در پردازشهای گسسته و جاهایی که نیاز به سرعت بالا داریم، از تابع fft استفاده میکنیم که با دقت خوبی و با سرعت بیشتر تبدیل فوریه توابع را حساب میکند. در این الگوریتم نیاز به نمونه برداری از سیگنال داریم (با فرکانس نمونه برداری Fs). به مثال زیر دقت کنید:
|
1 2 3 4 5 6 7 8 9 10 |
Fs = 1000; % فرکانس نمونه برداری T = 1/Fs; % تناوب نمونه برداری L = 1500; % طول سیگنال t = (0:L-1)*T; % بردار زمان S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); X = S + 2*randn(size(t)); Y = fft(X); |
تبدیل لاپلاس در متلب
تبدیل لاپلاس یک تابع در حوزهی زمان را با فرمول زیر محاسبه میکنند و آن را به حوزهی s میبرد. همانطور که قبلا اشاره شد میتوان با این کار معادلات دیفرانسیل را به معالات جبری تبدیل کرد و راحتتر آنها را حل نمود.
$ L{f(t)} = \int_{0}^{\infty }f(t).e^{-st}dt $
به سینتکس تابع لاپلاس در متلب توجه کنید:
|
1 |
laplace(f(t)) |
|
1 2 3 4 5 6 7 8 |
syms s t a b w laplace(a) laplace(t^2) laplace(t^9) laplace(exp(-b*t)) laplace(sin(w*t)) laplace(cos(w*t)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
ans = 1/s^2 ans = 2/s^3 ans = 362880/s^10 ans = 1/(b + s) ans = w/(s^2 + w^2) ans = s/(s^2 + w^2) |
معکوس تبدیل لاپلاس در متلب
برای این کار مانند تبدیل فوریه در متلب، تابع لاپلاس یک i اضافه خواهد داشت و از تابع ilaplace استفاده میکنیم. به مثالهای زیر توجه کنید:
|
1 2 3 4 5 6 7 8 |
syms s t a b w ilaplace(1/s^7) ilaplace(2/(w+s)) ilaplace(s/(s^2+4)) ilaplace(exp(-b*t)) ilaplace(w/(s^2 + w^2)) ilaplace(s/(s^2 + w^2)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
ans = t^6/720 ans = 2*exp(-t*w) ans = cos(2*t) ans = ilaplace(exp(-b*t), t, x) ans = sin(t*w) ans = cos(t*w) |