نوشتهای که میخوانید، ترجمهای از نوشتهی خانم Erica Klarreich است که روز آخر ماه آگوست ۲۰۲۰، در سایت Quanta Magazine منتشر شد. این نوشته به بررسی کامل و جالبی از مسئله مسیر مستقیم روی دوازده وجهی منتظم، که یک جسم افلاطونی است، میپردازد؛ همچنین کشفی جدیدی در مورد آن بیان میکند. در این مطلب، بخشهایی به ترجمهی نوشتهی خانم Klarreich اضافه شده است تا برخی از مفاهیم موجود در آن برای همهی مخاطبان فنولوژی واضحتر شود.
معرفی اجسام افلاطونی
با وجود اینکه ریاضیدانان بیش از ۲۰۰۰ سال به بررسی دقیق ساختار پنج جسم افلاطونی یعنی چهار وجهی منتظم، مکعب، هشت وجهی منتظم، دوازده وجهی منتظم و بیست وجهی منتظم پرداختهاند ولی باز هم چیزهای بسیاری وجود دارد که دربارهی آنها نمیدانیم. شاید تا به حال عبارت اجسام افلاطونی را نشنیده باشید اما احتمالاً با دیدن اسمهای بالا چیزهایی به یاد آوردهاید. به تصویر زیر توجه کنید:
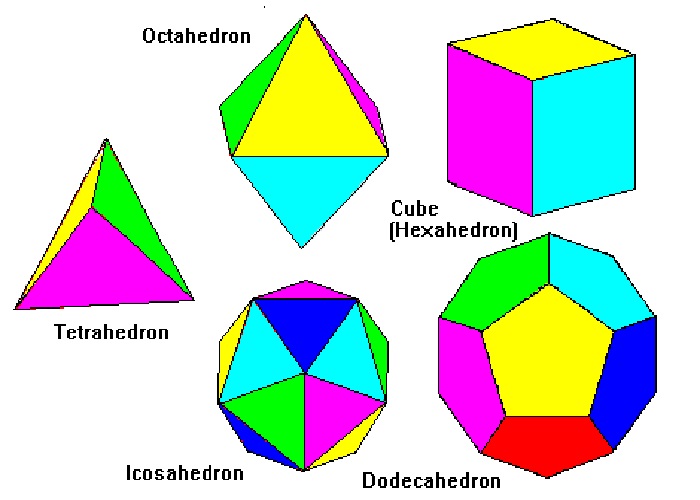
حال احتمالاً آنها را کاملاً به یاد آورده باشید. جزئیات و ویژگیهای بسیاری درمورد اجسام افلاطونی وجود دارد. ویژگیهایی که آنها را از اجسامی که شاید شبیه به اجسام افلاطونی باشند، متمایز میکند. ولی به طور خلاصه میتوان گفت که اجسام افلاطونی نوعی نسخهی سهبعدی از چندضلعیهای منتظماند.
البته وقتی از دو بعد، به سه بعد میرویم، پارامترهای بسیاری وجود دارد که با تغییر آنها میتوان اشکال حاصل را در دستههایی جداگانه تقسیم کرد؛ مثلاً تعداد رئوس، تعداد وجوه، شکل وجوه، تعداد یالها، زاویهی بین اضلاع و قطرهای گوناگون و … . اما بهطور خلاصه میتوان گفت که اجسام افلاطونی، منظمترینها در نوع خود، در سه بعد هستند.
توجه کنید که مثلا دوازده وجهی های دیگری به جز دوازده وجهی منتظم که افلاطونی است، وجود دارد ولی در این نوشته هرگاه از یک جسم $n$-وجهی نام بردیم، منظورمان همان جسم افلاطونی است.
مسئله مسیر مستقیم
فرض کنید روی یکی از رئوس یک جسم افلاطونی قرار دارید. آیا مسیر مستقیمی وجود دارد که آن را طی کنید و به نقطهی اولیه برگردید بدون اینکه از راسهای دیگر عبور کنید؟
منظور از یک مسیر مستقیم، مسیری است که خمیدگی و شکستگی در آن وجود نداشته باشد. البته واضح است که منظور از شکستگی، شکستگیهایی نیست که هنگام رفتن از یک وجه به وجه دیگر وجود دارد. وجود این نوع از شکستگیها در سه بعد، اجتناب ناپذیر است.
فرض کنید یکی از این اجسام افلاطونی را با مقوا ساختهاید و سپس آن را باز میکنید و میگسترانید؛ حال آنچه که در هنگام رفتن از یک وجه به وجه دیگر در سه بعد، به عنوان شکستگی دیده میشد، در این شکل دو بعدی چیزی به جز خط راستی که از یک چند ضلعی به چند ضلعی دیگری میرود، نیست.
پیشرفتهای قبلی در حل این مسئله مسیر مستقیم
این مسئله اخیراً (سال ۲۰۱۶) برای چهار وجهی، مکعب، هشت وجهی و بیست وجهی حل شده بود؛ البته به جز پاسخ به این پرسش، جزئیات بسیار بیشتری پیرامون این مسئله مشخص شده است. مقالهی مربوط به این کار را میتوانید در اینجا مشاهده کنید.
پاسخ این پرسش برای چهار جسم افلاطونی که نام بردیم، «خیر» است. هر مسیر مستقیمی، یا از یکی از رئوس دیگر عبور میکند یا تا ابد به گشتن روی وجوه ادامه میدهد، بدون این که به نقطهی شروع بازگردد. با این وجود، پاسخ مسئله مسیر مستقیم روی دوازده وجهی، که از دوازده پنج ضلعی منتظم ساخته شده، تا به امروز برای ریاضیدانان مشخص نبود.
تفاوت مسئله مسیر مستقیم روی دوازده وجهی با دیگر اجسام افلاطونی
به تازگی، سه ریاضیدان به نامهای Jayadev Athreya ،David Aulicino و Patrick Hooper نشان دادند که در واقع، بینهایت از این نوع مسیر مستقیم روی دوازده وجهی وجود دارد. مقالهی آنها که ماه می در ژورنال Experimental Mathematics منتشر شد، نشان داد که میتوان این مسیرها را به ۳۱ خانوادهی گوناگون تقسیم کرد.
در راهحل آنها از تکنیکها و الگوریتمهای کامپیوتری مدرنی استفاده شده است. Anton Zorich از موسسهی ریاضی Jussieu در پاریس میگوید:
«بیست سال پیش جواب دادن به این سوال، مطلقاً غیرممکن بود. ده سال پیش، نیاز به تلاش بسیار بزرگی بود تا همهی نرمافزارهای ضروری نوشته شوند و امروز همهی فاکتورها برای انجام این کار، دورهم گرد آمدند».
این پروژه سال ۲۰۱۶ آغاز شد؛ زمانی که Athreya از دانشگاه واشنگتن و Aulicino از کالج بروکلین، شروع به بازی با دستهای از تکههای مقوا کردند که با جمعشدن آنها، اجسام افلاطونی درست میشد. هرچه اجسام بیشتری ساختند، باعث میشد که Aulicino به این فکر کند که شاید کار آنها و دیگر پژوهشهای اخیر در مورد هندسهی مسطحه، همان چیزی باشد که برای درک مسیر مستقیم روی دوازده وجهی نیاز است. Athreya میگوید:
«ما این چیزها را دانه به دانه، کنار هم قرار دادیم؛ پس به گونهای میتوان گفت که پژوهشهای بیاساس ما به یک فرصت برای حل این مسئله تبدیل شد».
این دو ریاضیدان به همراه Hooper از کالج شهر نیویورک، متوجه شدند که چگونه میتوان همهی مسیرهای مستقیم را که بدون رد شدن از راس دیگری به نقطهی شروع باز میگردند، دستهبندی کرد. Howard Masur از دانشگاه شیکاگو میگوید:
«تحلیل آنها، یک راهحل بسیار ظریف و زیبا است. این یکی از آن چیزهایی است که بدون تردید میتوانم بگویم، ای کاش من آن را انجام داده بودم».

دوازده وجهی کاغذی که سال ۲۰۱۸ توسط Aulicino و Athreya ساخته شد تا مسیر مستقمی را نشان دهند که بدون رد شدن از راسهای دیگر، به نقطهی اولیه برمیگردد.
ویدئوی بررسی مسئله مسیر مستقیم روی دوازده وجهی
در ویدئویی که در اینجا قرار دارد، Athreya به بیان صورت مسئله مسیر مستقیم روی دوازده وجهی، ایدهها و چیزهای دیگری که با آنها درگیر بودهاند، میپردازد. از آنجا که در مسائل هندسه، خیلی خوب است که شهودی نسبت به حرفهای زده شده، داشته باشیم، توصیه میشود که این ویدئو را تماشا کنید؛ چون پر از تصاویر و انیمیشنهایی است که به درک بهتر مسئله، کمک میکنند.
این ویدئو، زیرنویس فارسی هم دارد. در آن همهی نکات مهمی که Athreya میگوید، نوشته شده است؛ ولی از ترجمهی برخی صحبتهای فرعی اجتناب شده است. همچنین بهتر است در برخی لحظات ویدئو، به انیمیشنها و تصاویری که نمایش داده میشود، دقت کنید تا صحبتها و زیرنویس. همچنین مطالبی مرتبط با صحبتهای موجود در ویدئو وجود دارد که خود داستانهای جداگانه دارند. افراد علاقهمند میتوانند که برخی از این مطالب مرتبط را در سایت Numberphile، که منتشر کنندهی این ویدئو نیز هست، دنبال کنند.
تقارنهای پنهان (Hidden Symmetries)
با وجود اینکه ریاضیدانان بیش از یک قرن در مورد مسئله مسیر مستقیم روی دوازده وجهی فکر میکنند، یک تجدید حیات دوباره در علاقه به این موضوع، در چند سال اخیر رخ داده است که دلیل این اتفاق، علاقه به درک «Translation Surface» ها بوده است. این سطوح (Surfaces)، با کنار هم گذاشتن ضلعهای موازی یک چندضلعی، به وسیلهی انتقال (Translation) ساخته میشوند و برای مطالعهی مباحثی که در آنها، مسیر مستقیم روی شکلهای گوشه دار مطرح است، مفید هستند. از جملهی این بحثها میتوان به مسئلههای مربوط به مسیرهای روی میز بیلیارد و مسئلهی روشن شدن تمام یک اتاقِ آینهکاری شده با یک لامپ، اشاره کرد.
در تمام این مسئلهها، ایدهی اصلی این است که شکل را باز کنیم؛ به گونهای که مطالعهی مسیرهای مورد نظرمان آسانتر شود. بنابراین برای درک مسیرهای مستقیم روی یک جسم افلاطونی، میتوانیم کار را با بریدن یالهای آن و باز کردن آن به صورت تخت روی یک سطح صاف، آغاز کنیم. ریاضیدانان به چنین شکلهای بازشدهای، Net میگویند. برای مثال یک نمونه Net برای مکعب، شکلی Tمانند است؛ مانند تصویر زیر:

البته واضح است که میتوانیم برای یک شکل، Net های دیگری نیز داشته باشیم.
تصور کنید یک دوازده وجهی را باز کرده و روی صفحه گستراندهایم. حال روی این سطح تخت، در مسیرهایی انتخابی، حرکت میکنیم؛ درنهایت به یکی از لبههای این Net میرسیم. در این نقاط، مسیر ما از پنج ضلعیای که در آن هستیم به پنج ضلعی دیگری جهش میکند که قبل از باز کردن دوازده وجهی با آن همسایه بوده است. هرگاه در مسیر ما چنین جهشهایی پیدا میشود، مسیر با زاویهای که مضرب صحیحی از ۳۶ درجه است، دوران پیدا میکند؛ شکل زیر یک نمونه Net برای دوازده وجهی است:
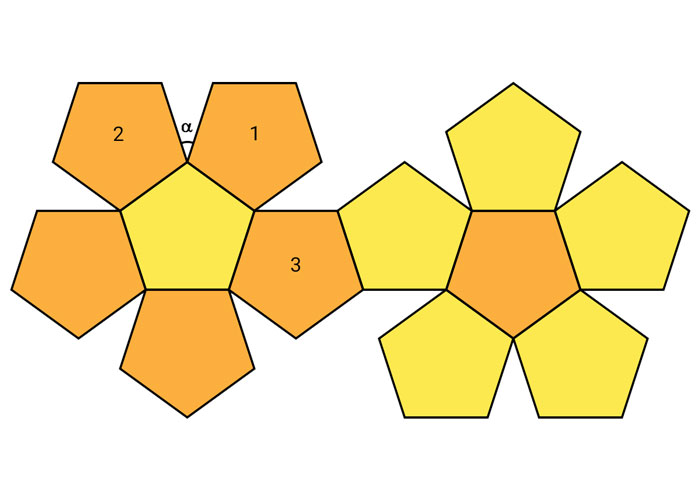
برای مثال دو پنج ضلعی شمارهی یک و دو در شکل را در نظر بگیرید. زاویههای هر پنج ضلعی منتظم، همگی ۱۰۸ درجهاند؛ پس به راحتی میتوان فهمید که زاویهی بین دو پنج ضلعی یعنی زوایهی $\alpha$ برابر با ۳۶ درجه است.
حال فرض کنید که یکی از مسیرهای ما در پنج ضلعی یک میرود و از آنجا جهش میکند. هر پنج ضلعی با پنج، پنج ضلعی دیگر، همسایه است. واضح است که پنج ضلعی شماره یک، با شماره دو و سه و پنج ضلعی مرکزی، همسایه است. از آنجا که پنج ضلعی شماره یک و پنج ضلعی مرکزی در یک ضلع به طور کامل مشترکاند، پس رفتن مسیر از یکی به دیگری همراه با جهش نخواهد بود.
اگر مسیر ما در ضلعی از پنج ضلعی شماره یک، که ضلعی از زاویهی $\alpha$ است، جهش کند، آنگاه مسیر، دورانی با زاویهی ۳۶ درجه خواهد داشت. به همین ترتیب اگر مسیر از پنج ضلعی شماره یک به سه جهش کند، دوران ۳۶ درجه ولی در جهت عکس (۳۶- درجه) خواهد داشت.
دو همسایهی دیگر برای پنج ضلعی شماره یک باقی میماند که این دو در قسمت راست شکل هستند. مشخص کردن زاویهی دوران مسیر در هنگام جهش به آنها کمی سختتر است، ولی چون تمام زاویههایی که با آنها سروکار داریم ۳۶ درجه و ۱۰۸ درجهاند، پس احتمالاً این زوایا نیز مضرب ۳۶ درجهاند. این موضوع برای Net های دیگر دوازده وجهی نیز صادق است. با دیدن انیمیشنهایی که در آن Net های دوازده وجهی تبدیل به دوازده وجهی میشوند، میتوان در مورد این زوایای دوران دید بهتری داشت. انیمیشن زیر، تشکیل شدن دوازده وجهی از Net بالا را نشان میدهد:
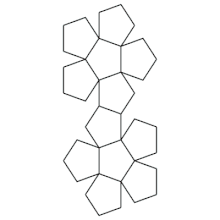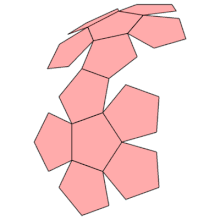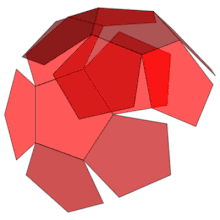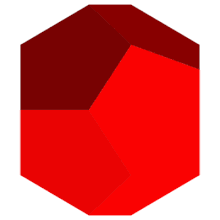
برای جلوگیری از همهی این جهشها و دورانها میتوان از یک ایدهی جالب استفاده کرد. چندین کپی از Net تهیه میکنیم و هرجا به لبههای Net اولیه رسیدیم، یکی از این Net ها را با زاویهی مناسب دوران داده و به محل اتمام مسیر در Net اولیه میچسبانیم. حال میتوان مسیر را در Net دوم ادامه داد، بدون اینکه مسیر جهش پیدا کند یا دورانی به مسیر بدهیم. همین موضوع را میتوانیم درمورد Net دوم و Net های بعدی ادامه دهیم. وقتی Net دوم را به اولی اضافه میکنیم، هر دو پنج ضلعی در مجموعهی حاصل، در واقع بیانگر یک پنج ضلعی در شکل اصلی است؛ در نتیجه با این کار دنیای خود را پیچیدهتر میکنیم ولی نمایش مسیرمان سادهتر میشود.
زمانی که مسیر ما ۱۰ تا از Net ها را طی کرد، Net اولیه را با تمام زاویههای ممکن که مضرب ۳۶ درجهاند، دوران میدهیم؛ سپس Net یازدهم را به گونهای اضافه میکنیم که هم جهت با Net اولیه باشد. به عبارتی Net یازدهم «انتقال یافته»ی Net اولیه خواهد بود؛ پس به جای اینکه Net یازدهم را اضافه کنیم، میتوانیم لبهی Net دهم که مسیر در آنجا پایان یافته، به لبهی موازی و متناظر با آن در Net اولیه بچسبانیم. حال دیگر شکل ما یک شکل تخت نیست اما ریاضیدانان به خاطر شکل قبلیش، هنوز به فرم یک شکل تخت به آن فکر میکنند؛ پس برای مثال، مسیر مستقیم در نظر گرفته میشود اگر در شکل تخت، مستقیم بوده باشد. بعد از این که همهی این لبههای موازی و متناظر ممکن را به هم چسباندیم، شکلی به دست خواهد آمد که به آن «Translation Surface» گفته میشود.
سطحی که به دست میآید، بسیار پیچیدهتر و اضافیتر از دوازده وجهی است؛ هر پنج ضلعی در دوازده وجهی منتظم، ۱۰ تا پنج ضلعی در این شکل خواهد بود. شکل حاصل مانند دوناتی میشود که ۸۱ سوراخ دارد. این شکل به این سه ریاضیدان اجازه داد تا مسئله مسیر مستقیم روی دوازده وجهی را به نظریهی Translation Surface ها ارتباط دهند.
ریاضیدانان به طور جدی مشغول شدند تا از عهدهی این سطح برآیند. بعد از چند ماه کار بر روی این مسئله، آنها متوجه شدند که این شکل نه تنها با دوازده وجهی، بلکه با یکی از Translation Surface هایی که تا آن زمان مورد مطاله و توجهِ بسیار بوده، نیز ارتباط دارد. نام این شکل، «Double Pentagon» است که از کنار هم گذاشتن دو پنج ضلعی از طریق یک ضلع مشترک، به وجود میآید؛ سپس با چسباندن ضلع های موازی این شکل به یکدیگر، میتوان یک دونات با دو سوراخ ساخت که تقارنهای بسیاری دارد. Double Pentagon شکلی است که روی دست Athreya تتو شده؛ او میگوید:
«Double Pentagon شکلی است که قبل از پرداختن به این مسئله نیز آن را میشناختم و به آن علاقه داشتم».
از آنجا که Double Pentagon و دوازده وجهی، geometric cousins هستند (نوعی ارتباط از نظر هندسی)، تقارنهای یکی میتواند تقارنهای دیگری را توضیح دهد. Alex Eskin از دانشگاه شیکاگو (استاد راهنمای Athreya در دوره دکتری) میگوید:
«این واقعیت که دوازده وجهی، چنین گروه تقارن پنهانی دارد، خیلی چشمگیر است».
ارتباط بین این سطوح به این معنی بود که ریاضیدانان میتوانستند از الگوریتم «analyzing highly symmetric translation surfaces» که ریاضیدانی آلمانی به اسم Myriam Finster روی آن کار کرده بود، نهایت استفاده را ببرند. با استفاده از این الگوریتم، ریاضیدانان توانستند که این مسیرها را پیدا کنند و آنها را با توجه به تقارنهای پنهان دوازده وجهی، دستهبندی کنند. Athreya میگوید:
«تحلیل این مسئله، یکی از فانترین پروژههایی است که در طول زندگی کاریام آن را انجام دادهام. این مهم است که مشغول بازی با شکلها شوید».
حل این مسئله نشان داد که بعد از هزاران سال مطالعه روی اجسام افلاطونی، هنوز هم رازهایی در مورد آنها وجود دارد که میتوان کشف کرد. Eskin میگوید:
«من فکر میکنم که حتی برای این سه ریاضیدان هم شگفتآور بوده که چیزی جدید در مورد دوازده وجهی بگویند».
منبع: Quanta Magazine






