آمار توصیفی و استنباطی | تفاوت آمار توصیفی و استنباطی در چیست؟11 دقیقه مطالعه

علم آمار، قلب آنالیز داده‌ها است. این علم به ما کمک می‌کند که روندها و الگو‌ها را شناسایی کنیم. به ما کمک می‌کند که نقشه بریزیم. در اصل روحی را در داده‌ها می‌دمد و به ما یاری می‌رساند تا در آن داده‌ها معنایی دریابیم. روش‌های آماری مستقلی که ما در آنالیز داده‌ها استفاده می‌کنیم بسیار زیاد هستند و فراتر از شمارش‌اند. به صورت کلی می‌توان آمار را به دو دسته کلی تقسیم کرد: آمار توصیفی و استنباطی. تا آخر این مقاله از فنولوژی با ما همراه باشید.

آمار توصیفی و استنباطی چیست؟

آمار محدوده‌ای است که ریاضی بر آن چیره شده و با مجموعه‌ها، سازمان‌ها، آنالیز‌ها، تفسیر‌ها، و ارائه داده‌ها سر‌وکار دارد. در واقع در بیش‌تر مواقع آنالیز داده‌ها همان آمار و احتمالات است. زمانی که ما از کلمه آنالیز داده‌ها استفاده می‌کنیم چیزی که در واقع منظورمان است آنالیز آماری یک مجموعه‌ای از داده یا داده‌ها است. از آنجایی که آمار از پایه‌های آنالیز داده‌ است، برای هر زمینه‌ای که در آن نیاز به آنالیز داده‌ها باشد نیز مورد نیاز است. از علم و روان‌شناسی گرفته تا بازاریابی و داروشناسی، دامنه پهناور تکنیک‌های آماری را به طور کلی می‌توان به دو بخش آمار توصیفی و استنباطی تقسیم کرد: ولی فرق این دو چیست؟ در ادامه به توضیح تفاوت‌های آمار توصیفی و استنباطی خواهیم پرداخت.

به طور خلاصه آمار توصیفی بر روی توصیف خصوصیات قابل رویت یک مجموعه از داده‌ها (یک جمعیت یا نمونه) تمرکز می‌کند. در همین حال آمار استنباطی تمرکز خود را بر روی ‌پیش‌بینی‌ها یا کلیت‌بخشی درباره یک مجموعه داده بزرگ‌تر بر اساس یک نمونه از داده های ذکر شده قرار می‌دهد.

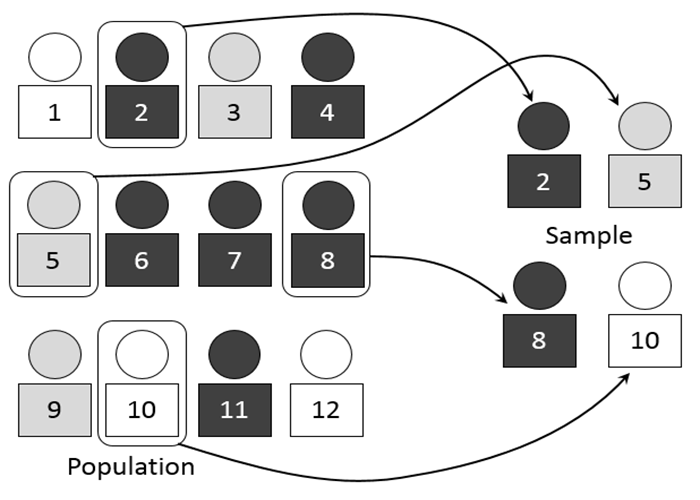
جمعیت و نمونه در آمار

دو موضوع ساده ولی ضروری در آمار و احتمالات جمعیت و نمونه هستند.

• جمعیت تمام گروهی است که شما می‌خواهید از آن‌ها داده خود را استخراج کنید (و در ادامه به نتیجه‌ای برسید). در حالی‌که در زندگی روزمره، این کلمه بیش‌تر برای توصیف جمعیتی از افراد (مانند جمعیت یک کشور) استفاده می‌شود، در آمار این کلمه برای هر گروهی که شما از آن‌ها اطلاعات گردآوری می‌کنید استفاده می‌شود. معمولا این جمعیت شامل افراد می‌شود ولی می‌تواند شهرهای جهان، حیوانات، اشیا، گیاهان، رنگ‌ها و چیزهای بسیار دیگری را نیز شامل شود.
• یک نمونه گروهی از نمایندگان یک جمعیت بزرگ‌تر است. نمونه‌برداری تصادفی از گروه‌های نماینده به ما اجازه می‌دهد تا نتیجه‌گیری گسترده در مورد جمعیت‌های بزرگ‌تر انجام دهیم. این رویکرد معمولا در نظرسنجی‌ها استفاده می‌شود. ناظران نظرسنجی از گروهی کوچک از مردم در مورد دیدگاهشان بر موضوعی مشخص پرس‌و‌جو می‌کنند. با اطلاعات به دست آمده می‌توان قضاوت‌های آگاهانه در مورد افکار جمعیت بزرگ‌تر انجام داد. به این گونه می‌توان در زمان، دشواری و هزینه های استخراج داده‌ها از تمام جمعیت (که عملا غیرممکن است) صرفه‌جویی کرد.

آمار توصیفی چیست؟

آمار توصیفی برای توصیف خصوصیات یا امکانات یک مجموعه از داده استفاده می‌شود. کلمه آمار توصیفی برای توصیف مشاهدات کمی فردی (آمار خلاصه) و همین‌طور روند کلی دستیابی به فهم این مجموعه از داده‌ها استفاده می‌شود. از آمار توصیفی می‌توان برای توصیف کل جمعیت یا یک نمونه خاص استفاده کرد. به خاطر توضیحی بودن این آمار، در آمار توصیفی خیلی نگران تفاوت‌های بین دو نوع از داده نیستند. معیارهایی که آمار توصیفی به آن‌ها نگاه می‌کند شامل توزیع، گرایش‌مرکزی و تنوع است.

توزیع چیست؟

توزیع تناوب نتایج مختلف (نقاط داده) یک جمعیت یا یک نمونه را به ما نشان می‌دهد که می‌توانیم آن را با اعداد در یک لیست و یا یک گراف نشان دهیم. برای مثال لیست زیر نشان‌دهنده تعداد افرادی است که از بین ۲۸۶ نفر چه رنگ مویی دارند.

• موی قهوه‌ای: ۱۳۰
• موی مشکی: ۳۹
• موی بلوند: ۹۱
• موی بور: ۱۳
• موی خاکستری: ۱۳

اطلاعات داده شده را می‌توان به صورت تصویری با نمودار پای نشان داد.

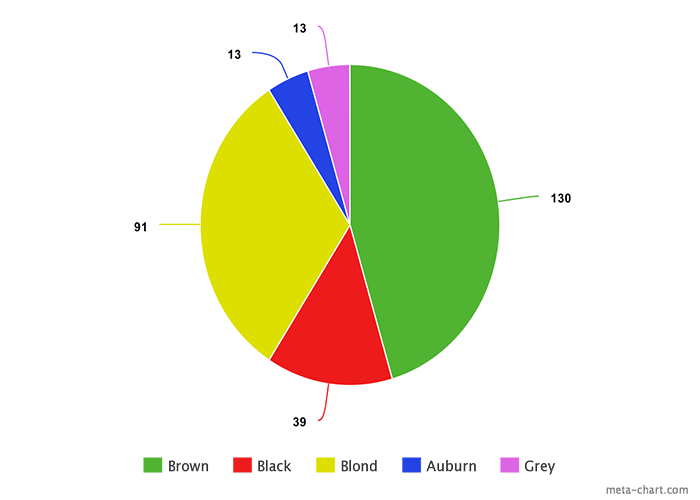
تصویری کردن نتایج آمار توصیفی معمول است. این مسئله به ما کمک می‌کند تا الگوها و روند‌های یک مجموعه داده را به راحتی شناسایی کنیم.

گرایش مرکزی چیست؟

گرایش مرکزی نام نوعی اندازه گیری است که به مقادیر مرکزی معمولی درون یک مجموعه داده می‌پردازد. این فقط مربوط به مقادیر مرکزی درون یک محموعه داده که به آن مدیان (متوسط) گفته می‌شود نیست، بلکه یک اصطلاح کلی است که برای توصیف اندازه‌گیری‌های مرکزی مختلف استفاده می‌شود. برای مثال، می‌تواند شامل اندازه گیری‌های مرکزی چارک مختلف یک مجموعه داده بزرگ‌تر باشد. معیارهای متداول گرایش مرکزی عبارتند از:

• میانگین: میانگین مقداری از همه نقاط داده
• میانه: مقدار میانی یک مجموعه داده
• مد: مقداری که دفعات بیش‌تری در مجموعه داده نمایان می‌شود

باری دیگر، با استفاده از مثال رنگ مو می‌توانیم دریابیم که میانگین ما ۵۷.۲ است (مقدار همه اندازه گیری‌ها تقسیم بر تعداد مقادیر). میانه ۳۹ است (مقدار وسطی داده‌ها) و مد ۱۳ است (به علت ظاهر شدن به تعداد دو بار در داده‌‌ها، که بیش‌تر از دیگر داده‌ها است). با این مثال ساده، در بسیاری از حوزه‌های آنالیز داده‌ها این اندازه گیری‌های مرکزی زیربنای خلاصه و تفسیر کردن ویژگی‌های یک نمونه و جمعیت است. خلاصه‌سازی این گونه از آمارها اولین قدم است در جهت تعیین‌کردن سایر خصوصیات مانند فراوانی داده‌ها.

تنوع در آمار توصیفی چیست؟

تنوع یا پراکندگی یک مجموعه داده نشان می‌دهد که چگونه داده‌ها پخش یا توزیع شده‌اند. شناسایی تنوع به شناخت اندازه‌گیری تمایل مرکزی یک مجموعه داده بستگی دارد. با این‌‌حال، مانند گرایش مرکزی، تنوع نیز فقط یک اندازه‌گیری نیست.  این کلمه‌ای است که برای توصیف دامنه‌ای از اندازه گیری‌ها به کار می‌رود. معیارهای متغیر متداول شامل موارد زیر است:

• انحراف معیار: این میزان تنوع یا پراکندگی را به ما نشان می‌دهد. انحراف معیار پایین به این معنی است که بیش‌تر مقادیر نزدیک به میانگین هستند. انحراف معیار بالا نشان می‌دهد که مقادیر به طور گسترده‌تری پخش شده‌اند.
• مقادیر مینیمم و ماکسیمم: این بالاترین و کم‌ترین مقادیر در یک مجموعه داده یا چارک هستند. با استفاده مجدد از مثال مجموعه داده رنگ مو، مینیمم و ماکسیمم مقادیر به ترتیب ۱۳ و ۱۳۰ می‌باشد.
• دامنه: این اندازه دامنه توزیع مقادیر را اندازه‌گیری می‌کند. با کم کردن کم‌ترین مقدار از بزرگ‌ترین، این مسئله به راحتی قابل تشخیص است. بنابراین، در مجموعه داده‌های رنگ مو ما، دامنه ۱۱۷ (۱۳۰ منهای ۱۳) است.
• درجه اوج در یک نمودار آماری (کورتوزیس یا Kurtosis): این شاخص نوسانات شدید در یک توزیع آماری را بررسی می‌کند؛ (همچنین به عنوان داده‌های پرت یا خطای آماری شناخته می‌شوند). اگر یک نمونه فاقد خطاهای آماری باشد، می‌توان گفت که دارای درجه اوج کم است. اگر یک مجموعه تعداد داده‌های پرت‌ها زیادی داشته باشد، می‌توان گفت که دارای درجه اوج زیاد است.
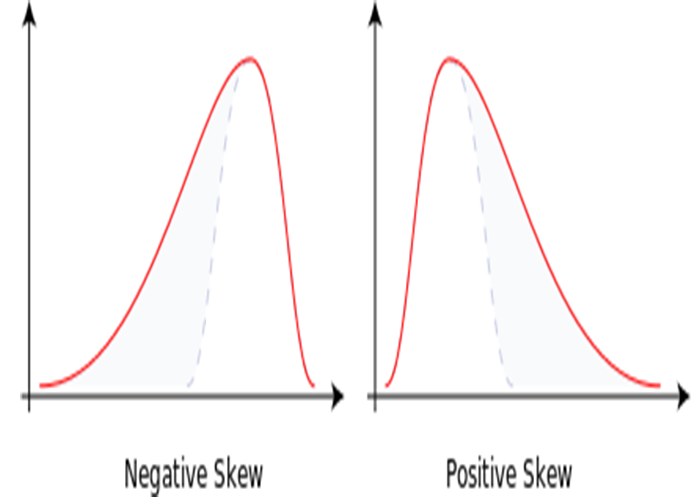
• کجی یا Skewness: این اندازه‌گیری تقارن مجموعه داده است. اگر می‌خواستید منحنی زنگوله‌ای طراحی کنید و خط دست راست بلندتر و چاق‌تر باشد، ما این را کجی مثبت می‌نامیم. اگر خط دست چپ بلندتر و چاق‌تر باشد، این را کجی منفی می‌نامیم. مانند تصویر زیر:

توزیع، گرایش مرکزی و تغییرپذیری با هم می‌تواند مقدار شگفت انگیزی از اطلاعات دقیق درباره یک مجموعه داده را به ما بگویند. در تجزیه و تحلیل داده‌ها، آن‌ها اقدامات بسیار رایجی هستند، به ویژه در زمینه تجزیه و تحلیل داده‌های اکتشافی. هنگامی که ویژگی‌های اصلی جمعیت یا نمونه را خلاصه کردید، در وضعیت بهتری قرار دارید که بدانید چگونه می‌توانید با آن کار کنید. و اینجاست که آمار استنباطی وارد می‌شود.

آمار استنباطی چیست؟

تا به اینجا، توضیح دادیم که آمار توصیفی بر خلاصه‌کردن ویژگی‌های اصلی یک مجموعه داده متمرکز است. از طرفی، آمار استنباطی بر ایجاد تعمیم در مورد جمعیت بیش‌تر بر اساس یک نمونه کوچک‌تر از آن جمعیت متمرکز است. از آنجا که آمار استنباطی بر پیش‌بینی (و نه بیان واقعیت‌ها) متمرکز است، نتایج آن معمولا به صورت یک احتمال است.

جای تعجب نیست که صحت آمار استنباطی تا حد زیادی به صحت و دقت نمونه‌های بزرگ جمعیت بستگی دارد. انجام این کار شامل به‌دست آوردن یک نمونه تصادفی است. اگر تا به حال اخبار مربوط به مطالعات علمی را خوانده باشید، قبلا با این اصطلاح روبرو شده اید. این نکته همیشه این است که نمونه‌گیری تصادفی به معنای نتایج بهتر است. در مقابل، نتایج حاصل از نمونه‌های مغرضانه یا غیر تصادفی معمولا استفاده نمی‌شوند. نمونه گیری تصادفی برای انجام تکنیک‌های استنباطی بسیار مهم است، اما همیشه ساده نیست.

چگونه یک نمونه تصادفی داشته باشیم؟

نمونه گیری تصادفی می‌تواند یک فرایند پیچیده باشد و اغلب به ویژگی‌های خاص یک جمعیت بستگی دارد. با این حال، اصول اساسی شامل موارد زیر است:

تعریف جمعیت

این به سادگی به معنای تعیین مجموعه‌ای است که می‌توانید نمونه خود را از آن بگیرید. همان‌طور که قبلا توضیح دادیم، یک جمعیت می‌تواند هر چیزی باشد؛ فقط به مردم محدود نمی‌شود. بنابراین می‌تواند جمعیتی از اشیا، شهرها، گربه‌ها، سگ‌ها یا هر چیز دیگری باشد که بتوانیم از آن اندازه‌گیری کنیم.

مشخص‌کردن اندازه نمونه

هرچه اندازه نمونه شما بزرگ‌تر باشد، نمایندگی بیش‌تری از کل جمعیت خواهد داشت. ترسیم نمونه‌های بزرگ می‌تواند زمان‌بر، دشوار و گران باشد. در‌واقع، به همین دلیل است که ما در وهله اول نمونه گیری می‌کنیم؛ به‌ندرت امکان تهیه داده‌ها از کل جمعیت وجود دارد. بنابراین اندازه نمونه شما باید به اندازه کافی بزرگ باشد تا بتوانید از نتایج خود اطمینان حاصل کنید؛ اما آنقدر کوچک نباشد که داده‌ها از دقت کافی برخوردار نباشند. این جایی است که استفاده از آمار توصیفی می‌تواند کمک کند، زیرا به ما امکان می‌دهد تعادلی بین اندازه و دقت ایجاد کنیم.

انتخاب تصادفی یک نمونه

هنگامی که اندازه نمونه را تعیین کردید، می‌توانید یک انتخاب تصادفی انجام دهید. ممکن است این کار را با استفاده از یک مولد اعداد تصادفی انجام دهید، به هر مقدار یک عدد اختصاص دهید و اعداد را به صورت تصادفی انتخاب کنید. یا می‌توانید این کار را با استفاده از طیف وسیعی از تکنیک‌ها یا الگوریتم‌های مشابه انجام دهید.

آنالیز نمونه داده

هنگامی که یک نمونه تصادفی دارید، می‌توانید از آن برای استنباط اطلاعات مربوط به جمعیت بیش‌تر استفاده کنید. توجه به این نکته مهم است که اگرچه یک نمونه تصادفی نماینده یک جمعیت است، اما هرگز ۱۰۰٪ دقیق نخواهد بود. به عنوان مثال، میانگین نمونه به ندرت با میانگین کل جمعیت مطابقت دارد، اما ایده خوبی در مورد آن به شما می‌دهد. به همین دلیل، مهم است که حاشیه خطای خود را در هر تجزیه و تحلیل لحاظ کنید. به همین دلیل همان‌طور که قبلا توضیح داده شد، هر نتیجه‌ای از فنون استنباطی به صورت یک احتمال است. با این حال، با فرض این‌که نمونه تصادفی به دست آورده‌ایم، بسیاری از تکنیک‌های استنباطی برای تجزیه و تحلیل و به‌دست آوردن بینش از این داده‌ها وجود دارد. این لیست طولانی است، اما برخی از تکنیک‌های قابل توجه عبارتند از:

• آزمایش فرضیه
• فاصله اطمینان
• رگرسیون و تحلیل همبستگی

آزمایش فرضیه چیست؟

آزمایش فرضیه بررسی می‌کند نمونه‌های شما نتایج فرضیه شما را تکرار می‌کنند یا خیر. هدف این است که نتایج مثبتی که به طور تصادفی اتفاق افتاده‌اند را از نمونه آماری جدا کنیم. یک مثال، از این آزمایشات بالینی واکسن کرونا است. از آنجا که انجام آزمایشات روی کل جمعیت غیرممکن است، در عوض آزمایشات متعددی را بر روی چندین نمونه تصادفی انجام می‌دهیم.

در این مورد، آزمایش فرضیه ممکن است از این قبیل سوال کند: آیا واکسن شدت بیماری ناشی از کرونا را کاهش می‌دهد؟ با جمع‌آوری داده‌ها از گروه‌های مختلف نمونه، می‌توان نتیجه گرفت که آیا واکسن موثر است. اگر همه نمونه‌ها نتایج مشابهی را نشان دهند و ما بدانیم که آن‌ها تصادفی هستند، می‌توانیم تعمیم دهیم که واکسن همان تأثیر را روی جمعیت کل خواهد داشت. از طرف دیگر، اگر یک نمونه کارایی بالاتر یا کم‌تری از نمونه‌های دیگر نشان می‌دهد، باید دلیل این مسئله را بررسی کنیم. به عنوان مثال، ممکن است اشتباهی در روند نمونه‌گیری رخ داده باشد، یا شاید واکسن به گونه متفاوتی به آن گروه منتقل شده باشد. در واقع، به دلیل خطای اندازه‌گیری مقدار واکسن باشد که یکی از واکسن‌های کرونا کارآمدتر از سایر گروه‌ها در آزمایش باشد؛ که نشان می‌دهد آزمایش فرضیه تا چه اندازه مهم است. اگر این نمونه ضعیف وجود نداشت، اثر واکسن کم‌تر بود.

فاصله اطمینان چیست؟

از فواصل اطمینان برای برآورد پارامترهای خاصی برای اندازه گیری جمعیت (مانند میانگین) بر اساس داده‌های نمونه استفاده می‌شود. به جای ارائه یک مقدار متوسط، فاصله اطمینان طیف وسیعی از مقادیر را فراهم می‌کند. این غالبا به صورت درصدی آورده می‌شود. اگر تا به حال مقاله علمی پژوهشی خوانده اید، نتیجه گیری‌های حاصل از یک نمونه همیشه با فاصله اطمینان همراه است.

به عنوان مثال، بگذارید بگوییم شما طول دم ۴۰ گربه انتخاب شده به طور تصادفی را اندازه گیری کرده‌اید. طول متوسط دم‌ها ۱۷.۵ سانتی‌متر است. شما همچنین می‌دانید که انحراف معیار طول دم ۲ سانتی متر است. با استفاده از یک فرمول خاص، می‌توانیم بگوییم متوسط طول دم در کل جمعیت گربه‌ها ۱۷.۵ سانتی‌متر است، با فاصله اطمینان ۹۵ درصد. اساسا، این به ما می‌گوید که ما ۹۵٪ اطمینان داریم که میانگین جمعیت (که بدون اندازه گیری کل جمعیت نمی‌توانیم بدانیم) در محدوده داده شده قرار دارد. این روش برای اندازه‌گیری درجه دقت در یک روش نمونه‌گیری بسیار مفید است.

رگرسیون و تحلیل همبستگی چیست؟

رگرسیون و تحلیل همبستگی هر دو روش مورد استفاده برای مشاهده چگونگی ارتباط دو (یا بیش‌تر) مجموعه متغیرها با یکدیگر هستند. تجزیه و تحلیل رگرسیون با هدف تعیین تأثیر یک متغیر وابسته (یا خروجی) توسط یک یا چند متغیر مستقل (یا ورودی) انجام می‌شود. این اغلب برای آزمایش فرضیه و تجزیه و تحلیل پیش‌بینی استفاده می‌شود. به عنوان مثال، برای پیش بینی فروش ضد‌آفتاب (یک متغیر خروجی) ممکن است فروش سال گذشته را با داده‌های هواشناسی (که هر دو متغیر ورودی هستند) مقایسه کنید تا ببینید میزان فروش در روزهای آفتابی چقدر افزایش یافته است.

در همین حال، تحلیل همبستگی، میزان ارتباط بین دو یا چند مجموعه داده را اندازه‌گیری می‌کند. برخلاف تحلیل رگرسیون، همبستگی علت و معلول را استنباط نمی‌کند. به عنوان مثال، فروش بستنی و آفتاب سوختگی هر دو احتمالا در روزهای آفتابی بیش‌تر خواهد بود که می‌توان گفت همبستگی دارند. اما درست نیست اگر بگوییم بستنی باعث آفتاب سوختگی می‌شود.

آنچه در اینجا توضیح دادیم، فقط بخش کوچکی از تعداد زیادی تکنیک استنباطی است که می‌توانید در تجزیه و تحلیل داده‌ها استفاده کنید. با این حال، آن‌ها طعم دلچسب نوعی از قدرت پیش‌بینی را که آمار استنباطی می‌تواند ارائه دهد، فراموش نمی‌کنند.

چه تفاوتی بین آمار استنباطی و توصیفی وجود دارد؟

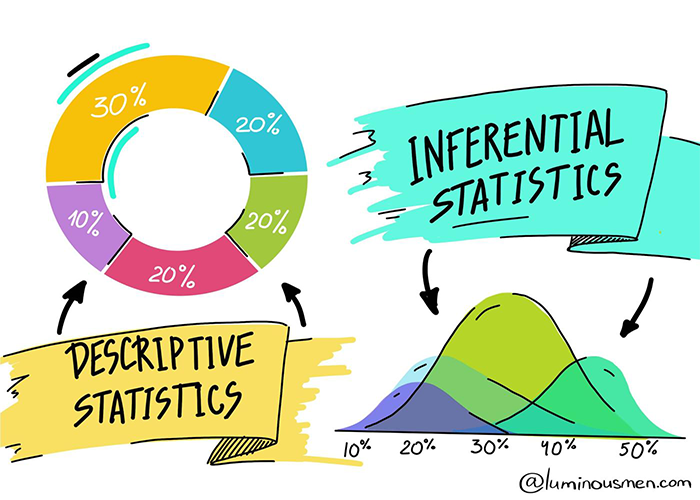
آمار توصیفی

• ویژگی‌های جمعیت‌ها و یا نمونه‌ها را توصیف می‌کند.
• داده‌ها را به صورت کاملا واقعی سازماندهی و ارائه می‌دهد.
• نتایج نهایی را با استفاده از جداول و نمودارها ارائه می‌دهد.
• براساس داده‌های شناخته شده نتیجه گیری می‌کند.
• از اقداماتی مانند گرایش مرکزی، توزیع و واریانس استفاده می‌کند.

آمار استنباطی

• از نمونه‌ها برای ایجاد تعمیم در مورد جمعیت‌های بزرگ‌تر استفاده می‌کند.
• برای تخمین و پیش‌بینی نتایج آینده به ما کمک می‌کند.
• نتایج نهایی را به صورت احتمالات ارائه می‌دهد.
• نتیجه‌گیری که فراتر از داده‌های موجود می‌باشد را نشان می‌دهد.
• از تکنیک‌هایی مانند تست فرضیه‌، فواصل اطمینان و تحلیل رگرسیون و همبستگی استفاده می‌کند.

آخرین نکته ای که باید به آن توجه کنید، در حالی که ما آمار توصیفی و استنباطی را به صورت مجزا ارائه دادیم‌، اما در واقع آن‌ها اغلب به صورت مشترک استفاده می‌شوند. روی هم رفته‌، این تکنیک‌های آماری قدرتمند که شامل آمار توصیفی و استنباطی نیز هستند‌، بستری اساسی است که تجزیه و تحلیل داده بر روی آن بنا شده است.

منبع: CAREEFOUNDRY