مساحت دایره را چگونه محاسبه کنیم؟ | همراه با اثبات4 دقیقه مطالعه

دایره یکی از اشکال هندسی است که اثر آن از دیرباز در آثار هنری، سازه‌ها و محیط پیرامون دیده شده است. گاهی اوقات پیش می‌آید که در امور مهندسی یا فنی نیاز داریم تا مساحت دایره را محاسبه کنیم. گاهی اوقات نیز سطح مورد نظر خود را به طور تقریبی مانند دایره فرض می‌کنیم تا بتوانیم اندازه مساحت آن را به دست آوریم. در این مقاله از فنولوژی، رابطه‌ای که برای محاسبه مساحت دایره به کار می‌رود را اثبات می‌کنیم. با ما همراه باشید.

دایره چیست؟

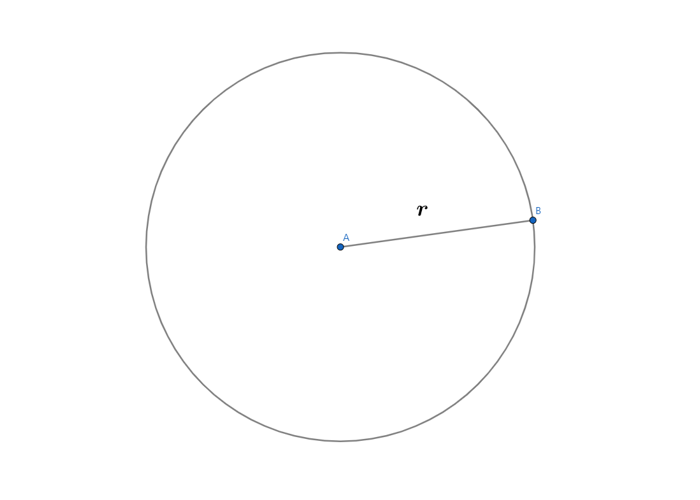
دایره را می‌توان مجموعه نقاطی در نظر گرفت که از یک نقطه خاص که «مرکز دایره» نامیده می‌شود، فاصله یکسانی دارند. به این فاصله، اندازه شعاع دایره می‌گویند.

به بیانی دیگر، شعاع دایره پاره خطی است که یک سر آن مرکز دایره و یک سر دیگر آن بر روی محیط دایره قرار دارد. پس می‌توان نتیجه گرفت که هر دایره در صفحه با دو مشخصه شناخته می‌شود. مشخصه اول، مختصات مرکز دایره و مشخصه دوم، اندازه شعاع آن است.

مساحت دایره را می‌توان به وسیله‌ی رابطه‌ی زیر محاسبه کرد. در این رابطه، r اندازه شعاع دایره است.

$S = \pi r^2$

از حسابان می‌دانیم که هر دایره در صفحه که مختصات مرکز آن به صورت (a , b) باشد و اندازه شعاع آن نیز r باشد را می‌توان به صورت زیر نشان داد:

$x – a)^2 + (y – b)^2 = r^2$)

واضح است که رابطه بین x و y، تابعی ایجاد نمی‌کند.

مساحت دایره را چطور محاسبه کنیم؟ | اثبات

حال نوبت به این می‌رسد که مساحت دایره را به دست آوریم. نکته‌ای که باید به آن توجه کنیم، این است که مساحت دایره، هیچ ارتباطی به مختصات مرکز آن ندارد. لذا برای ساده‌تر شدن محاسبات، فرض می‌کنیم که مرکز دایره‌ی مورد نظر ما، بر روی مبدا مختصات قرار دارد. در نتیجه:

$x^2 + y^2 = r^2$

رویکردی که برای محاسبه مساحت به کار می‌گیریم استفاده از انتگرال است. زیرا می‌دانیم اگر انتگرال یک تابع را بر روی بازه مشخصی، نسبت به محور x محاسبه کنیم، در واقع مساحت محصور بین آن منحنی و محور x را به دست آورده‌ایم. در این‌جا رابطه‌ای که برای دایره داریم، تابع نیست؛ لذا باید ابتدا این مشکل را حل کنیم. به مراحل زیر توجه کنید.

$x^2 + y^2 = r^2$

$y^2 = r^2 – x^2$

$y = \pm \sqrt{r^2 – x^2}$

برای اینکه بتوانیم از انتگرال استفاده کنیم، می‌توانیم از تابع $f(x) = \sqrt{r^2 – x^2}$ روی بازه صفر تا r، برای محاسبه مساحت ناحیه بالای محور x انتگرال بگیریم. سپس با چهار برابر کردن مقدار به دست آمده، مساحت دایره به دست می‌آید. پس خواهیم داشت:

$ \frac{\mathrm{S} }{\mathrm{4}} = \intop\nolimits_{0}^{r} (\sqrt{r^2 – x^2}) dx $

حال یک تغییر متغیر اعمال می‌کنیم.

$x = r\sin(t)$

$dx = r\cos(t)dt$

بازه انتگرال نیز از ۰ تا r به ۰ تا $ \frac{\mathrm{ \pi } }{\mathrm{2}} $ تغییر می‌یابد.

مقادیر x و dx را بر حسب t جایگزین می‌کنیم. خواهیم داشت:

$\frac{\mathrm{S} }{\mathrm{4}} = \intop\nolimits_{0}^{r} \sqrt{r^2 – x^2}) dx$

$ = \intop\nolimits_{0}^{ \frac{\mathrm{ \pi } }{\mathrm{2}} } (\sqrt{r^2 – (r\sin(t))^2}. r\cos(t)dt$

$ = \intop\nolimits_{0}^{ \frac{\mathrm{ \pi } }{\mathrm{2}} } r.\sqrt{1 – (\sin(t))^2}. r\cos(t)dt$

$ = \intop\nolimits_{0}^{ \frac{\mathrm{ \pi } }{\mathrm{2}} } r^2.\cos^2(t)dt$

حالا از رابطه طلایی استفاده می‌کنیم. یعنی:

$\frac{\mathrm{(1 + \cos (2t))} }{\mathrm{2}} = \cos ^2(t)$

در نتیجه:

$= \intop\nolimits_{0}^{ \frac{\mathrm{ \pi } }{\mathrm{2}} } r^2.( \frac{1 + \cos (2t)}{2})dt$

انتگرال به دست آمده را می‌توانیم محاسبه کنیم. به این ترتیب خواهیم داشت:

$ \frac{\mathrm{S} }{\mathrm{4}} = \intop\nolimits_{0}^{ \frac{\mathrm{ \pi } }{\mathrm{2}} } r^2.( \frac{1 + \cos (2t)}{2})dt$

محاسبه انتگرال نامعین عبارت زیر را نتیجه می‌دهد:

$ = \frac{\mathrm{r^2} }{\mathrm{2}}.(t + \frac{\mathrm{1} }{\mathrm{2}} .\sin (2t)) + C$

آن را در بازه ۰ تا $ \frac{\mathrm{ \pi } }{\mathrm{2}} $ محاسبه می‌کنیم.

$ \frac{\mathrm{S} }{\mathrm{4}} = \frac{\mathrm{r^2} }{\mathrm{2}}.( \frac{\mathrm{ \pi } }{\mathrm{2}} + \frac{\mathrm{1} }{\mathrm{2}} .\sin ( \pi )) – \frac{\mathrm{r^2} }{\mathrm{2}}.(0 + \frac{\mathrm{1} }{\mathrm{2}} .\sin (0))$

$ \frac{\mathrm{S} }{\mathrm{4}} = \frac{\mathrm{r^2} }{\mathrm{2}}.\frac{\mathrm{ \pi } }{\mathrm{2}} = \frac{\mathrm{ r^2 \pi } }{\mathrm{4}}$

اگر طرفین تساوی را در ۴ ضرب کنیم، مساحت به دست می‌آید:

$S = \pi r^2$

بر اساس عبارت به دست آمده می‌توان نتیجه گرفت که مساحت هر دایره با مربع اندازه شعاع آن رابطه مستقیم دارد. برای مثال اگر شعاع یک دایره ۳ برابر بزرگ‌تر شود، مساحت آن ۹ برابر می‌شود.

مثال از محاسبه مساحت دایره

فرض کنید قصد داریم مساحت یک قسمت دایره‌ای‎‌شکل به شعاع ۳ متر را محاسبه کنیم. طبق رابطه‌ای که به دست آوردیم، کافی است مربع اندازه شعاع را در عدد پی ضرب کنیم:

$S = \pi . 3^2 = 9 \pi \backsimeq 28.27$

لذا مساحت این دایره حدودا ۲۸.۲۷ متر مربع است.

در این مطلب، ابتدا دایره را تعریف کردیم. سپس مشخص کردیم با چه رابطه‌ای می‌توان آن را در صفحه و روی دستگاه مختصات نشان داد. در نهایت با استفاده از انتگرال توانستیم مساحت هر دایره را محاسبه کنیم. نتیجه‌ی محاسبات به این صورت بود که مساحت هر دایره با مربع اندازه شعاع آن رابطه مستقیم دارد.